Fractions

Autres Fiches Conceptuelles

Posez une Question

(+)

Votre Publicité sur le Réseau

Traduction

Fractions (Français) / Fractions (Anglais) / الكسور (Arabe)

(+)

Traductions

Définition

Domaine, Discipline, Thématique

(+)

Mathématiques / Arithmétique / Calcul /

Justification

Définition écrite

• Les fractions sont des nombres qui représentent la division de deux nombres entiers. Elles sont souvent notées sous la forme "a/b", où "a" et "b" sont des nombres entiers (appelés numérateur et dénominateur, respectivement).
• Par exemple:

            * la fraction 3/4 représente la division de 3 par 4, soit 0,75. 
            * La fraction 5/2 représente la division de 5 par 2, soit 2,5.

• Voici quelques exemples de fractions et comment les lire :

                                *  1/2  on lit: (un demi).
                                *  3/4  on lit: (trois quarts).
                                *  5/8  on lit: (cinq huitièmes).
                                *  7/1  on lit: (sept entiers).

(+)

En français, fraction signifie « morceau » ou « partie ». * Ainsi: *une fraction d'un gâteau, c'est un morceau, une part de ce gâteau. *Fractionner quelque chose signifie le mettre en morceaux. *En mathématiques, on appelle fraction une part d'une quantité (unité) que l'on a coupée en parts égales. * Le nombre du haut s'appelle le numérateur de la fraction. Il indique le nombre de parts que l'on prend ou que l'on veut représenter. * Le nombre du bas s'appelle le dénominateur de la fraction. Il indique en combien on a partagé l'unité, c'est-à-dire le nombre total de parts. *On peut ajouter, soustraire, multiplier et diviser des fractions entre elles, à condition de respecter certaines règles. * Par exemple: * pour ajouter des fractions, il faut d'abord s'assurer que leurs dénominateurs sont identiques, puis ajouter les numérateurs. * Pour soustraire des fractions, il faut d'abord s'assurer que leurs dénominateurs sont identiques, puis soustraire les numérateurs

Fractions - Historique (+)

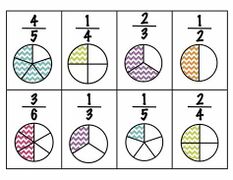
Définition graphique

• 

  quelques fractions

• 

  forme générale d'une fraction

• 

  fractions et vie

{{{AutresMedias}}}

Concepts ou notions associés

(+)

* La notion de valeur numérique: une fraction a une valeur numérique qui peut être calculée en divisant le numérateur par le dénominateur. / * Une fraction peut être simplifiée en divisant les numérateurs et dénominateurs par leur plus grand commun diviseur (PGCD). / * La notion de fraction équivalente: des fractions sont dites équivalentes si elles ont la même valeur numérique, même si les numérateurs et dénominateurs sont différents. / * La notion de fraction réduite: une fraction est dite réduite lorsque le numérateur et le dénominateur sont premiers entre eux. / * La comparaison des fractions: Les fractions peuvent être comparées en comparant leurs valeurs numériques ou en les réduisant à la même forme réduite. / * La notation mixte: Certaines fractions peuvent être notées de manière mixte, qui est la combinaison d'une fraction avec un nombre entier. / * Les opérations sur les fractions: les fractions peuvent être additionnées, soustraites, multipliées et divisées en respectant certaines règles et procédures. /

Fractions - Glossaire / (+)

Exemples, applications, utilisations

La cuisine: les recettes peuvent utiliser des fractions pour indiquer les quantités des ingrédients. **Par exemple, "1/2 tasse de sucre" signifie que l'on doit utiliser la moitié d'une tasse de sucre. Les mesures: les fractions sont souvent utilisées pour mesurer des longueurs, des distances et des angles. **Par exemple, une feuille de papier A4 est généralement divisée en quart pour faire des plis. La médecine: les fractions sont utilisées pour décrire les doses de médicaments. **Par exemple, une dose de 0,5 mg de médicament est équivalente à 1/2 milligramme. Les finances: Les fractions sont utilisées pour calculer les intérêts et les pourcentages. **Par exemple, si vous avez un taux d'intérêt de 3/4%, cela signifie que vous obtenez 3/4% de intérêts sur votre argent. Les sciences: Les fractions sont utilisées pour décrire les proportions et les pourcentages. **Par exemple, un mélange contenant 1/4 de sucre et 3/4 d'eau a 25% de sucre. Les arts: Les fractions sont utilisées pour décrire les proportions dans les œuvres d'art telles que les photographies ou les peintures. Géométrie : les fractions sont utilisées pour décrire les aires et les volumes des figures. les statistiques : Les fractions peuvent être utilisées pour décrire des proportions de données, telles que la proportion de personnes d'une certaine tranche d'âge dans une population. Dans le cadre de la répartition de l'héritage, les fractions peuvent être utilisées pour calculer les parts de chaque héritier. (+)

Erreurs ou confusions éventuelles

Erreur: Croire que

• une fraction représente deux entiers a part
• une fraction et toujours supérieure a 1

Confusion possible ou glissement de sens

• Confusion entre Numérateur - Dénominateur
• Confusion entre Fraction - Division

Erreur fréquente:

• L'addition de deux fractions est réalisée par la somme des numérateurs et celle des dénominateurs.
• Ne pas remarquer les égalités entre les fractions.
• Difficulté à simplifier les fractions.
• Ne pas donner de sens aux fractions et donc se trouver coincé lorsque le numérateur et supérieur au dénominateur.
• Ne pas mettre les fractions sous le même dénominateur ( voir numérateur ) avant de les comparer ce qui entraîne les fautes.
• Oubli de simplifier une fraction. Par exemple, si vous avez la fraction 5/10 et que vous oubliez de la simplifier en 1/2, votre calcul sera incorrect.
• Erreur de calcul lors de l'addition ou de la soustraction de fractions. Par exemple, si vous avez les fractions 3/4 et 1/2 et que vous les additionnez sans s'assurer que leurs dénominateurs sont identiques, votre calcul sera incorrect.
• Erreur de calcul lors de la multiplication ou de la division de fractions. Par exemple, si vous avez les fractions 3/4 et 1/2 et que vous les multipliez sans multiplier leurs numérateurs entre eux et leurs dénominateurs entre eux, votre calcul sera incorrect.
• Oubli de vérifier le résultat final. Il est important de vérifier le résultat final de votre calcul pour vous assurer qu'il est correct. Si vous oubliez de le faire, vous risquez de trouver un résultat qui est incorrect.
• Erreur de conversion de fractions en décimaux ou vice versa. Si vous faites une erreur lors de la conversion d'une fraction en décimal ou d'un décimal en fraction, votre calcul sera incorrect.

Il est important de prendre le temps de bien comprendre les règles de manipulation des fractions et de faire attention lors de vos calculs pour éviter ces erreurs courantes.

(+)

Questions possibles

• Qu'est-ce qu'une fraction et comment est-elle écrite?
• Comment calculer la valeur numérique d'une fraction?
• Comment simplifier une fraction en utilisant le PGCD?
• Comment comparer des fractions et déterminer si elles sont équivalentes?
• Comment additionner et soustraire des fractions en ayant le même dénominateur?
• Comment multiplier et diviser des fractions?
• Comment convertir une fraction en décimale?
• Comment convertir une décimale en fraction?
• Comment utiliser les fractions pour résoudre des problèmes de la vie réelle?
• Comment utiliser les fractions pour calculer les parts dans l'héritage?

(+)

Liaisons enseignements et programmes

Idées ou Réflexions liées à son enseignement

Voici les principales règles à connaître pour travailler avec des fractions:

• Pour ajouter ou soustraire des fractions, il faut d'abord s'assurer que leurs dénominateurs sont identiques. Si ce n'est pas le cas, il faut les "recaler" en multipliant leur numérateur et leur dénominateur par un même nombre, de façon à obtenir des fractions avec un dénominateur commun. Par exemple:

(3/4) + (1/2) = (3 x 2)/(4 x 2) + (1 x 4)/(2 x 4) = 6/8 + 4/8 = 10/8

• Pour multiplier des fractions, il suffit de multiplier leur numérateur entre eux et leur dénominateur entre eux. Par exemple:

(3/4) x (1/2) = 3 x 1 / 4 x 2 = 3/8

• Pour diviser des fractions, il faut inverser le second fraction (c'est-à-dire mettre le dénominateur en numérateur et le numérateur en dénominateur) et multiplier les deux fractions obtenues. Par exemple:

(3/4) / (1/2) = (3/4) x (2/1) = 3 x 2 / 4 x 1 = 6/4 = 3/2

• Pour simplifier une fraction, il faut diviser son numérateur et son dénominateur par leur plus grand diviseur commun. Par exemple:

15/25 = 15/5 x 5/5 = 3/5

Il est important de bien comprendre ces règles et de les respecter lors de vos calculs avec des fractions pour éviter des erreurs courantes.

(+)

Aides et astuces

• Pratiquez régulièrement les opérations sur les fractions, en utilisant des outils tels que des feuilles d'exercices ou des jeux en ligne pour renforcer la compréhension.

• Utilisez des visualisations pour aider à comprendre les fractions, telles que des fractions colorées ou des modèles en trois dimensions.

• Apprenez à utiliser et effectuer des opérations sur les fractions, et pour convertir les fractions en décimales et vice versa.

• Utilisez des comparaisons pour montrer comment les fractions sont similaires ou différentes les unes des autres.

• Faites des exercices de correspondance pour aider à comprendre les relations entre les fractions, les décimales et les pourcentages.

• Faites des exercices de résolution de problèmes pour aider à comprendre comment les fractions sont utilisées dans la vie quotidienne.

• Utilisez des outils tels que des fractions numériques pour montrer les liens entre les différentes formes de représentation des fractions.

• Poser des questions et à explorer les fractions de différentes manières pour renforcer leur compréhension.

Education: Autres liens, sites ou portails

• Apprendre les mathématiques (https://apprendrelesmathematiques.com/) : ce site en français propose des cours, des exercices et des vidéos sur les fractions pour les élèves de tous âges.

• Les mathématiques pour tous (https://www.lesmaths.net/) : ce site en français propose des cours, des exercices et des vidéos sur les fractions pour les élèves de tous âges.

• الرياضيات للجميع (https://math4all.net/) : ce site en arabe propose des cours, des exercices et des vidéos sur les fractions pour les élèves de tous âges.

• الرياضيات بالعربية (https://www.maths-arabic.com/) : ce site en arabe propose des cours, des exercices et des vidéos sur les fractions pour les élèves de tous âges.

• الرياضيات الجديدة (https://www.mathnew.net/) : ce site en arabe propose des cours, des exercices et des vidéos sur les fractions pour les élèves de tous âges.

• الأسئلة الشائعة في الرياضيات (https://www.mathq.net/) : ce site en arabe propose des réponses à des questions fréquentes sur les fractions pour les élèves de tous âges.

Bibliographie

Pour citer cette page: ([1])

ABROUGUI, M & al, 2023. Fractions. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Fractions>, consulté le 1, novembre, 2024

• Fractions, décimales et pourcentages pour les Nuls" de Mark Ryan : Ce livre fournit une introduction claire et concise aux fractions, décimales et pourcentages pour les élèves de tous âges.

• "Fractions, décimales et pourcentages : une introduction" de David A. Adler : Ce livre pour les élèves de tous âges fournit une introduction aux fractions, décimales et pourcentages, et comprend des exemples et des exercices pour renforcer la compréhension.

• "Fractions : une introduction pour les élèves de niveau élémentaire" de Rebecca Wingard-Nelson : Ce livre pour les élèves de niveau élémentaire fournit une introduction aux fractions, avec des exemples simples et des activités pour renforcer la compréhension.

• "Fractions : une introduction pour les élèves de niveau intermédiaire" de Susan O'Connell : Ce livre pour les élèves de niveau intermédiaire fournit une introduction aux fractions, avec des exemples et des activités pour renforcer la compréhension.

• "Fractions : une introduction pour les élèves de niveau avancé" de Harold Jacobs : Ce livre pour les élèves de niveau avancé fournit une introduction aux fractions, avec des exemples et des activités pour renforcer la compréhension.

• "Découvrir les fractions" de Michel Balazard, Jean-Paul Delahaye, et Nathalie Sinclair : Ce livre est un ouvrage de référence pour les enseignants pour aider les élèves à comprendre les fractions dans un contexte mathématique général, il est pratique pour les élèves de tous âges.

• المنشّط في الرياضيات (سنة خامسة و سنة سادسة) من إعداد ثلة من المربين التونسيين
• فكر و أنجز (سنة خامسة و سنة سادسة) من إعداد ثلة من المربين التونسيين
• تمارين وحلول (سنة خامسة و سنة سادسة) من إعداد ثلة من المربين التونسيين

Donnez votre avis sur les fiches conceptuelles