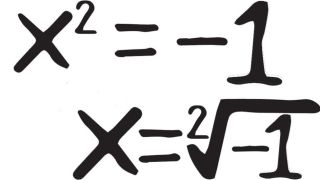Complexité des objets mathématiques

Fiches Question - Réponse

Posez une Question

Votre Publicité sur le Réseau

(+)

Conception : Clarification - Explicitation

Conceptions canoniques

• Confusion entre la didactique et la pédagogie :

La didactique des mathématiques est souvent confondue avec la pédagogie. La première se concentre sur les contenus mathématiques et leur structuration dans un cadre éducatif, tandis que la pédagogie concerne les méthodes générales d'enseignement. Par exemple, une activité ludique pour enseigner les fractions relève davantage de la pédagogie que de la didactique.

• Erreur conceptuelle liée aux obstacles épistémologiques :

Un obstacle épistémologique est une difficulté propre à la nature des concepts mathématiques. Par exemple, les élèves interprètent souvent l'infini comme un "nombre très grand" plutôt que comme un concept non quantifiable. Cette confusion résulte de la manière dont les savoirs mathématiques sont transposés dans le cadre éducatif.

• Difficulté d'interprétation entre savoir savant et savoir enseigné :

Le savoir savant est issu de la recherche scientifique et académique, tandis que le savoir enseigné est adapté aux capacités des apprenants. Par exemple, enseigner le théorème de Pythagore au collège implique une simplification par rapport à son énoncé rigoureux dans un cadre universitaire. Cette adaptation peut entraîner des malentendus chez l'enseignant ou l'élève.

• Nuance entre une erreur et une misconception :

Une erreur est un résultat incorrect ponctuel, alors qu’une misconception est une idée fausse persistante liée à une mauvaise compréhension. Par exemple, résoudre "2x + 3 = 7" en ajoutant "3" des deux côtés est une erreur. Mais penser que toute équation s’équilibre toujours de cette manière est une misconception.

• • Comparaison entre erreurs et obstacles** :

Les erreurs sont généralement des écarts par rapport à une réponse attendue, alors que les obstacles reflètent une limitation structurelle ou cognitive. Par exemple, une erreur de calcul dans la résolution d’une équation est différente de l’obstacle épistémologique lié à la compréhension des équations abstraites.

• Complexité du langage mathématique :

Les symboles et terminologies mathématiques peuvent être source de confusion. Par exemple, le symbole "=" est parfois interprété par les élèves comme "donne comme réponse" au lieu d’être compris comme une relation d’équivalence. Cette difficulté découle des spécificités du langage mathématique.

• • Comparaison entre langage naturel et langage symbolique** :

Le langage naturel permet une explication intuitive des concepts, mais peut entraîner des ambiguïtés. En revanche, le langage symbolique est précis mais souvent abstrait, créant des barrières pour les apprenants.

---

Conceptions erronées et origines possibles

• ...............................................................................

................................................................................ ................................................................................

(+)

Conceptions liées - Typologie

(+)

Confusion entre didactique et pédagogie / Erreur dans l’interprétation du langage mathématique / Confusion entre savoir savant et savoir enseigné / Difficulté avec les obstacles épistémologiques / Nuance entre une erreur et une misconception / Problème de transposition didactique / Confusion entre intuition et raisonnement formel / Complexité liée au contrat didactique implicite / Mauvaise interprétation des représentations graphiques / Confusion entre langage naturel et langage symbolique /

Concepts ou notions associés

Références Liens éducatifs relatifs aux 5 Mots-Clés Principaux
Sur le Portail Questions / Réponses - Questions / Réponses - Questions / Réponses - Questions / Réponses - Questions / Réponses - Questions / Réponses	Sur Portail de Formation Gratuite - Formation - Formation - Formation - Formation - Formation	Sur des sites de Formation - Multisites Educatifs - Multisites Educatifs - Multisites Educatifs - Multisites Educatifs - Multisites Educatifs	Sur DidaQuest - Sur DidaQuest - Sur DidaQuest - Sur DidaQuest - Sur DidaQuest - Sur DidaQuest
Complexité des objets mathématiques sur : Wikipedia / Wikiwand / Universalis / Larousse encyclopédie / Khan Académie
Sur Wikiwand : [1] / [2] / [3] / [4] / [5]
Sur Wikipédia : [6] / [7] / [8] / [9] / [10]
Sur Wikiversity : [11] / [12] / [13] / [14] / [15]
Sur Universalis : [16] / [17] / [18] / [19] / [20]
Sur Khan Académie : [21] / [22] / [23] / [24] / [25]

Éléments graphique

• 

  Image 1

• 

  Image 2

• 

  Image 3

• AUTRES MEDIAS

Modèle:Complexité des objets mathématiquesModèle:Complexité des objets mathématiques (Discipline)
Modèle:Complexité des objets mathématiques: (Discipline)
Modèle:Complexité des objets mathématiquesModèle:Complexité des objets mathématiques: (Discipline)
Complexité des objets mathématiques: (Discipline)
Modèle:Complexité des objets mathématiques: (Discipline)
Complexité des objets mathématiques
Modèle:Complexité des objets mathématiques Modèle:Complexité des objets mathématiques
Représentation graphique spatiale Modèle:Complexité des objets mathématiques: carte conceptuelle (cmap)
Document PDF Modèle:Complexité des objets mathématiques: Document PDF
Image/Figure Modèle:Complexité des objets mathématiques: Complexité des objets mathématiques

Stratégie de changement conceptuel

Voici des stratégies pour favoriser des changements conceptuels et dissiper des obstacles en mathématiques :

• Clarification de la distinction entre didactique et pédagogie:

Il est important de commencer par expliciter la différence entre didactique et pédagogie pour éviter la confusion. - Exemple : Expliquer que la **didactique** se concentre sur la **structure des connaissances** et la manière dont elles doivent être enseignées, tandis que la **pédagogie** englobe des approches plus larges de l'enseignement, y compris la gestion de la classe et les stratégies motivationnelles.

• Transposition didactique simplifiée:

Pour éviter la confusion sur la transposition didactique, on peut utiliser des exemples concrets de transposition de concepts mathématiques. - Exemple : Montrer comment un concept abstrait, comme les fonctions, est simplifié en classe avec des graphiques ou des tables de valeurs, avant d'être approfondi dans un contexte plus théorique.

• Utilisation d’analogies pour surmonter les obstacles épistémologiques:

Les analogies peuvent aider à comprendre des concepts difficiles en les reliant à des expériences quotidiennes. - Exemple : Utiliser l'analogie du "compte-gouttes" pour expliquer les concepts d'infini ou de limites, en comparant un goutte à goutte d’eau qui semble infini mais n’est en fait qu’une petite portion d'un tout.

• Explicitation du langage mathématique:

Clarifier le langage mathématique dès le début pour éviter que les élèves n’interprètent mal les symboles. - Exemple : Au lieu de simplement dire que "x = 5", montrer que cela signifie "x est équivalent à 5" et non "x donne 5", afin de souligner la relation d’équivalence.

• Distinguer les erreurs et misconceptions:

Il est crucial de démontrer comment certaines erreurs proviennent de mauvaises interprétations persistantes. - Exemple : Après une erreur de calcul sur les fractions, discuter des raisons sous-jacentes et proposer des activités pour déconstruire la misconception, comme en utilisant des représentations visuelles.

• Renforcement du contrat didactique:

Clarifier les attentes implicites entre enseignant et élèves peut lever des confusions. - Exemple : Présenter explicitement ce que l'enseignant attend de l'élève, et vice versa, dans le cadre d'un problème mathématique, en soulignant l'importance des démarches et du raisonnement, pas seulement des résultats.

• Démonstration de l’importance du raisonnement formel:

Amener les élèves à distinguer clairement l’intuition du raisonnement rigoureux. - Exemple : Montrer un raisonnement informel sur les propriétés des triangles, puis le vérifier rigoureusement avec les théorèmes associés, afin que les élèves comprennent que l'intuition doit être justifiée par des preuves formelles.

• Exercices sur les représentations graphiques:

Utiliser des exercices pratiques qui relient les graphiques aux équations. - Exemple : Demander aux élèves de dessiner des graphiques et de déterminer les équations associées pour des fonctions simples, afin de leur faire comprendre la relation entre représentation géométrique et algébrique.

• Utilisation de la reformulation pour résoudre les erreurs de compréhension:

Encourager les élèves à reformuler les questions ou problèmes dans leurs propres mots pour clarifier leurs incompréhensions. - Exemple : Après une erreur dans la résolution d’une équation, demander à l’élève de reformuler l’énoncé en d’autres termes pour mieux saisir le problème.

• Pratique du feedback constructif:

Le feedback doit non seulement corriger les erreurs mais aussi expliquer pourquoi une démarche est incorrecte et proposer des solutions concrètes. - Exemple : Lorsque les élèves commettent une erreur dans une opération, non seulement donner la bonne réponse, mais aussi expliquer en quoi la méthode initiale était erronée et proposer des alternatives plus efficaces.

Ces stratégies, accompagnées d'exemples pratiques, peuvent aider à surmonter les obstacles d’apprentissage en mathématiques et à améliorer la compréhension des élèves.

(+)

Questions possibles

• Quelle est la différence entre la didactique et la pédagogie ? : La didactique se concentre sur le contenu disciplinaire et ses méthodes d'enseignement, tandis que la pédagogie traite des approches générales de l'enseignement.

• Qu'est-ce que la transposition didactique ? : C'est le processus par lequel un savoir savant est transformé en un savoir enseignable adapté au contexte éducatif.

• Comment les obstacles épistémologiques influencent-ils l'apprentissage des mathématiques ? : Ils peuvent créer des incompréhensions persistantes dues à la nature abstraite et historique des concepts mathématiques.

• Quelles sont les principales erreurs liées au langage mathématique ? : Une erreur fréquente est de confondre "=" comme "donne la réponse" au lieu de "établit une équivalence".

• En quoi consiste le contrat didactique ? : Il désigne les attentes implicites entre l'enseignant et l'élève sur leurs rôles respectifs dans le processus d'apprentissage.

• Pourquoi est-il important de différencier une erreur d’une misconception ? : Une erreur est ponctuelle et corrigible immédiatement, alors qu'une misconception traduit une compréhension incorrecte persistante.

• Comment le langage naturel peut-il créer des confusions en mathématiques ? : Les formulations intuitives peuvent parfois contredire la rigueur des définitions mathématiques, entraînant des malentendus.

• Quels sont les défis liés à l’enseignement des représentations graphiques ? : Les élèves peuvent avoir des difficultés à faire le lien entre les propriétés géométriques visibles et les concepts mathématiques abstraits.

• Qu'est-ce que l'intuition en mathématiques, et en quoi se distingue-t-elle du raisonnement formel ? : L'intuition repose sur des perceptions immédiates ou des exemples concrets, tandis que le raisonnement formel suit une logique rigoureuse et abstraite.

• Comment évaluer les conceptions erronées chez les élèves en mathématiques ? : Cela peut se faire en analysant leurs réponses à des tâches complexes et en identifiant les raisonnements sous-jacents incorrects.

(+)

Bibliographie

Pour citer cette page: (des objets mathématiques)

ABROUGUI, M & al, 2024. Complexité des objets mathématiques. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Complexit%C3%A9_des_objets_math%C3%A9matiques>, consulté le 23, décembre, 2024

• ..................
• ..................
• ..................
• ..................

Donnez votre avis sur les fiches conceptuelles

Votre Publicité sur le Réseau