Nombre Complexe
De Didaquest
Révision datée du 6 mai 2017 à 10:55 par Mouajriamarwa (discussion | contributions) (Page créée avec « {{widget:NavigationFicheConceptuelle}} {{widget:HautFicheConceptuelle}} {{widget:PBEducation}}<!-- La syntaxe suivante ne doit pas être modifiée--> = {{Widget:Traductio... »)
 Traduction
Traduction
 Définition
Définition
Domaine, Discipline, Thématique
|
Mathématique / Géométrie / les angles / Exponentielle / Forme Algébrique / Module / Argument / Forme géométrique / .... / ....
|
Définition écrite
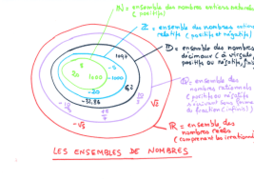
- On admet qu'il existe un ensemble de nombres, noté C, qui contient l'ensemble des nombres réels R vérifiant les propriétés suivantes :
- C contient un nombre noté i tel que i² = -1;
- tous les éléments de C s'écrivent de manière unique sous la forme
a + ib où a et b sont des nombres réels ;
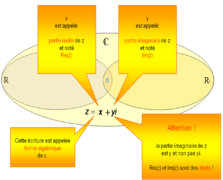
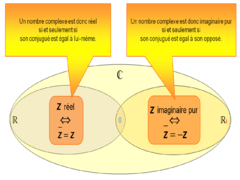
L'écriture de ses éléments z sous la forme a + ib où a et b sont des nombres réels est appelée écriture algébrique du complexe z. Le nombre a s'appelle la partie réelle de z, b est sa partie imaginaire. On utilisera les notations suivantes : Re(z) = a et Im(z) = b. |
Définition graphique
 Concepts ou notions associés
Concepts ou notions associés
 Exemples, applications, utilisations
Exemples, applications, utilisations
• Soit les complexes z = 2 - 3i et z' = 1 + i. Z + z'=2 - 3i + 1 + i = 3 - 2i z x z' = (2 - 3i) (1 + i) = 2 + 2i - 3i – 3i² = 2 - i - 3 x (-1) = 5 - i • i3 = i² × i = -i ; i4= (i²)² = 1. |
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
 Questions possibles
Questions possibles
- Trouver l'écriture algébrique d'un nombre complexe ?
- Comment passe de la forme exponentielle à la forme trigonométrique et réciproquement?
- Interpréter graphiquement un nombre complexe?
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
Education: Liens, sites et portails
- URL :
Difficultés liées à son enseignement
- Convaincre les élèves qu'il existe un nombre tel que son carré est négatif.
Aides et astuces
- Un petit coup de pouce : Si A,B et C sont alignés, alors l'angle orienté(AB,BC)=[0]
- Il existe un moyen de déterminer deux nombres en connaissant leurs produit et leur somme. Cependant, il n'est accessible qu'aux élèves à partir de la première car il faut savoir résoudre une équation du second degré.
- Si a+b = S et ab = P, alors a et b sont les deux solutions de l'équation x² - Sx + P = 0.
- Si le discriminant est positif, l'équation a deux solutions : ce sont les valeurs a et b. Cependant, sans autres indications sur a et b, on ne peut pas déterminer quelle solution vaut a et quelle solution vaut b.
- Si le discriminant est nul, l'équation n'a qu'une solution, les deux nombres a et b valent cette solution.
- Si le discriminant est négatif, il n'existe aucun couple de nombres réels ayant la somme et le produit donnés (mais, si vous connaissez, il existe des nombres complexes qui conviennent).
- Preuve : l'équation « x² - (a+b)x + ab = 0 » équivaut à « (x-a)(x-b) = 0 » et a donc pour solutions a et b.
 Bibliographie
Bibliographie
- L'odyssée
- Legendre