Nombre Complexe
De Didaquest
Aller à la navigationAller à la rechercheThe printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
 Traduction
Traduction
 Définition
Définition
Domaine, Discipline, Thématique
|
Mathématique / Géométrie / les angles / Exponentielle / Forme Algébrique / Module / Argument / Forme géométrique / .... / ....
|
Définition écrite
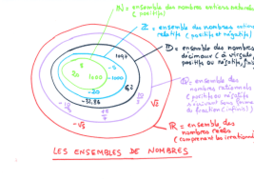
- On admet qu'il existe un ensemble de nombres, noté C, qui contient l'ensemble des nombres réels R vérifiant les propriétés suivantes :
- C contient un nombre noté i tel que i² = -1;
- tous les éléments de C s'écrivent de manière unique sous la forme
a + ib où a et b sont des nombres réels ;
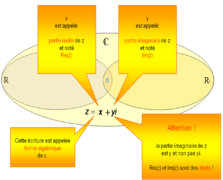
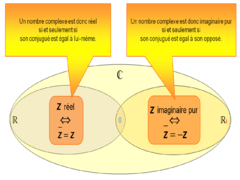
L'écriture de ses éléments z sous la forme a + ib où a et b sont des nombres réels est appelée écriture algébrique du complexe z. Le nombre a s'appelle la partie réelle de z, b est sa partie imaginaire. On utilisera les notations suivantes : Re(z) = a et Im(z) = b. |
Définition graphique
 Concepts ou notions associés
Concepts ou notions associés
 Exemples, applications, utilisations
Exemples, applications, utilisations
• Soit les complexes z = 2 - 3i et z' = 1 + i. Z + z'=2 - 3i + 1 + i = 3 - 2i z x z' = (2 - 3i) (1 + i) = 2 + 2i - 3i – 3i² = 2 - i - 3 x (-1) = 5 - i • i3 = i² × i = -i ; i4= (i²)² = 1. |
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
 Questions possibles
Questions possibles
- Trouver l'écriture algébrique d'un nombre complexe ?
- Comment passe de la forme exponentielle à la forme trigonométrique et réciproquement?
- Interpréter graphiquement un nombre complexe?
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
Education: Liens, sites et portails
- URL :
Difficultés liées à son enseignement
- Convaincre les élèves qu'il existe un nombre tel que son carré est négatif.
Aides et astuces
- Un petit coup de pouce : Si A,B et C sont alignés, alors l'angle orienté(AB,BC)=[0]
- Il existe un moyen de déterminer deux nombres en connaissant leurs produit et leur somme. Cependant, il n'est accessible qu'aux élèves à partir de la première car il faut savoir résoudre une équation du second degré.
- Si a+b = S et ab = P, alors a et b sont les deux solutions de l'équation x² - Sx + P = 0.
- Si le discriminant est positif, l'équation a deux solutions : ce sont les valeurs a et b. Cependant, sans autres indications sur a et b, on ne peut pas déterminer quelle solution vaut a et quelle solution vaut b.
- Si le discriminant est nul, l'équation n'a qu'une solution, les deux nombres a et b valent cette solution.
- Si le discriminant est négatif, il n'existe aucun couple de nombres réels ayant la somme et le produit donnés (mais, si vous connaissez, il existe des nombres complexes qui conviennent).
- Preuve : l'équation « x² - (a+b)x + ab = 0 » équivaut à « (x-a)(x-b) = 0 » et a donc pour solutions a et b.
 Bibliographie
Bibliographie
- L'odyssée
- Legendre