Valeurs centrales

Autres Fiches Conceptuelles

Posez une Question

(+)

Votre Publicité sur le Réseau

Traduction

Valeurs centrales (Français) / Concept en Anglais (Anglais) / Concept en Arabe (Arabe)

(+)

Traductions

Définition

Domaine, Discipline, Thématique

(+)

Statistiques / Probabilités / Mathématiques /

Justification

Définition écrite

• Nombre qui caractérise le centre d’une distribution et la position des diverses valeurs de la distribution par rapport à ce centre.

Les principales mesures de tendance centrale sont la moyenne arithmétique, la médiane et le mode.

• Les valeurs centrales (mode, médiane, moyenne) sont des indicateurs statistiques simples d'emploi que l'on retrouve au cœur de toute exploration de données (Sciences des données). Elles permettent notamment de définir une norme à partir de laquelle il devient possible de comparer les différents individus de la population étudiée. Il est donc important de les connaître et savoir laquelle choisir.

(+)

Valeurs centrales - Historique (+)

Définition graphique

• 

  Titre de Votre Image 1

• 

  Titre de Votre Image 2

• 

  Titre de Votre Image 3

{{{AutresMedias}}}

Concepts ou notions associés

(+)

Mode / Médiane / Moyenne /

Valeurs centrales - Glossaire / (+)

Exemples, applications, utilisations

La distribution ci-dessous donne la liste des âges des 25 élèves d’une classe de 6e année. 10, 10, 11, 11, 11, 11, 11, 11, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 13, 13, 13, 13, 13 La moyenne est : Moy = 29525 = 11,8 La médiane est : Méd = 12 Le mode est : Mod = 12 (+)

Erreurs ou confusions éventuelles

• Choix et pertinences : Moyenne - Mode - Médiane
• Confusion entre: Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique

(+)

Questions possibles

• .................. ?
• .................. ?
• .................. ?

(+)

Liaisons enseignements et programmes

Idées ou Réflexions liées à son enseignement

• ..................

• .................

• ..................

• .................

(+)

Aides et astuces

• Les propriétés de Yule

Le statisticien George Udny Yule a défini six propriétés souhaitables pour les valeurs centrales :

• Être définie de façon objective : deux personnes différentes traitant la même information doivent trouver le même résultat en ce qui concerne le calcul des valeurs centrales. Ceci est vrai pour la moyenne et la médiane mais pas pour le mode qui dépend du choix de l’amplitude de la classe adoptée.
• Dépendre de toutes les observations : la modification d'une seule observation doit entraîner une modification de la valeur centrale. Ceci est le cas de la moyenne mais pas du mode et de la médiane.
• Avoir une signification concrète : bien que la moyenne paraisse "naturelle" elle est en fait très abstraite alors que le mode peut être défini comme la situation la "plus fréquente" et la médiane comme celle "qui divise en deux la distribution" (un individu sur deux a une valeur inférieure ou supérieure à celle-ci).
• Être simple à calculer : toutes les valeurs centrales sont simples à calculer.
• Être peu sensibles aux fluctuations d'échantillonage : cette propriété définit la robustesse de la mesure face à des erreurs qui peuvent apparaître (données mal codées, valeurs aberrantes/extrêmes). La moyenne "explose" en présence d'une valeur extrême alors que la médiane est très robuste. Le mode est en situation intermédiaire.
• Se prêter au calcul algébrique : la moyenne se prête au calcul algébrique, ce qui n'est pas le cas du mode et de la médiane.

Propriétés de Yule	Mode	Médiane	Moyenne
Être définie de façon objective	-	+	+
Dépendre de toutes les observations	-	-	+
Avoir une signification concrète	+	+	-
Être simple à calculer	+	+	+
Être peu sensibles aux fluctuations d'échantillonage	-	+	+
Se prêter au calcul algébrique	-	-	+

En suivant ces différents critères il n'y a donc pas de valeur centrale parfaite, mais alors comment faire un choix ? Tout dépend de la forme de la distribution étudiée.

Valeurs centrales et formes de distribution

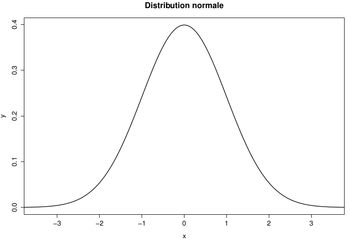
• Distribution normale

Quand la distribution est symétrique, elle se rapproche d'une loi normale. Les trois valeurs centrales sont alors les mêmes et peuvent être utilisées indistinctement, mais on préfère souvent utiliser la moyenne.

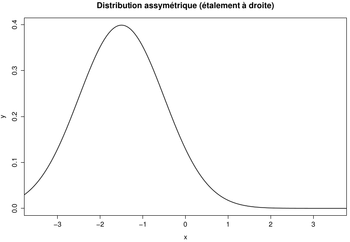
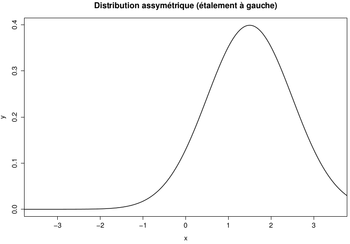
• Distribution asymétrique (à droite ou à gauche)

Lorsque la distribution est asymétrique quelques individus aux valeurs extrêmes contribuent à étaler la courbe vers la droite ou la gauche. Dans ce type de situation il faut utiliser la médiane.

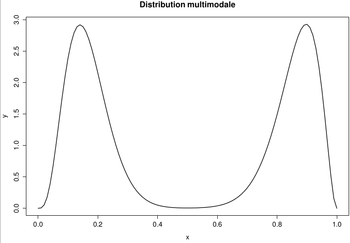
• Distribution multimodale

Lorsqu'il y a plusieurs zones de concentration principales des valeurs, alors la distribution est dite multimodale. On utilise alors les différents modes pour résumer l'information.

Education: Autres liens, sites ou portails

• ..................
• ..................
• ..................

Bibliographie

Pour citer cette page: (centrales)

ABROUGUI, M & al, 2018. Valeurs centrales. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Valeurs_centrales>, consulté le 21, novembre, 2024

• ..................
• ..................
• ..................
• ..................

Donnez votre avis sur les fiches conceptuelles