Différences entre versions de « Fonction affine »
| Ligne 197 : | Ligne 197 : | ||
{{@}} '''Confusion possible ou glissement de sens''' | {{@}} '''Confusion possible ou glissement de sens''' | ||
| − | * Confusion entre [[ | + | * Confusion entre [[Fonction affine - Fonction linéaire]] |
| − | * Confusion entre [[ | + | * Confusion entre [[Fonction constante - Fonction affine]] |
| − | * Confusion entre [[ | + | * Confusion entre [[Parallèle - Perpendiculaire]] |
| − | * Confusion entre [[ | + | * Confusion entre [[Inéquations linéaires - Equations linéaires]] |
| − | * Confusion entre [[ | + | * Confusion entre [[Fonction affine - Equation de droite]] |
| − | * Confusion entre [[ | + | * Confusion entre termes [[Linéaire - Affine]] |
| − | * Confusion entre [[ | + | * Confusion entre [[Fonctions affines - Fonctions quadratiques]] |
Version du 9 décembre 2023 à 14:08
 Votre Publicité sur le Réseau
|
Traduction
Traductions
Définition
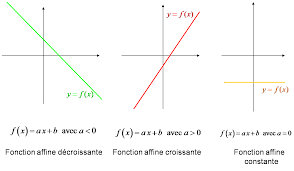
Une fonction affine est une fonction mathématique qui représente une relation linéaire entre une variable indépendante "x" et une variable dépendante "f(x)". Elle est définie par l'équation f(x) = ax + b, où "a" est la pente de la droite correspondante, et "b" est l'ordonnée à l'origine. La pente "a" détermine la raideur de la relation linéaire, et l'ordonnée à l'origine "b" indique la valeur de la fonction lorsque la variable indépendante est zéro. Les fonctions affines sont couramment utilisées pour modéliser des relations linéaires dans divers domaines, et elles sont représentées par des droites dans un plan cartésien.
Domaine, Discipline, Thématique
Mathématiques / Économie / Finance / Physique / Ingénierie / Statistiques / Informatique / Gestion / Géographie / Chimie / Biologie / Psychologie / Éducation / Architecture / Musique /
Justification
Définition écrite
{{Fiche Didactique Definition |Définition=
- Une fonction affine est une fonction mathématique qui peut être représentée par une équation de la forme :
f(x)=ax+b ou a et b sont des constantes réelles, et x est la variable indépendante. Dans cette équation Le coefficient a représente la pente de la fonction, c'est-à-dire la variation de la fonction par unité de variation de la variable indépendante. La constante b est l'ordonnée à l'origine, c'est-à-dire la valeur de la fonction lorsque la variable indépendante est égale à zéro L'expression ax+b peut également être interprétée géométriquement comme l'équation d'une droite dans le plan cartésien. La fonction affine décrit donc une relation linéaire entre la variable indépendante x et la variable dépendante f(x), où chaque variation constante de x entraîne une variation proportionnelle de f(x)
|Typologie=
Définition graphique
fonction affine maher 1
fonction affine maher 2
fonction affine maher 3
- AUTRES MEDIAS
affine Fonction affine
affine Fonction affine
Représentation graphique spatiale Fonction affine
Concepts ou notions associés
Fonction affine / Coefficient directeur (a) / Ordonnée à l'origine (b) / Droite affine / Relation linéaire / Droite parallèle et droite perpendiculaire / Intersection de droites / Inéquations linéaires / Régression linéaire / Domaine et codomaine / Image / Pente et ordonnée à l'origine / Parallélisme et perpendicularité / Racine et zéro de la fonction / Fonction constante / Inversibilité / Variation linéaire /
Fonction affine - Glossaire / (+)
Exemples, applications, utilisations
Fonctions de demande : Les fonctions affines peuvent être utilisées pour modéliser la demande de produits en fonction de leur prix. Une relation linéaire simple peut être utile pour prédire comment la demande varie avec les prix.
Modélisation financière : Les fonctions affines peuvent être utilisées pour modéliser la croissance des investissements, le calcul des intérêts composés et d'autres aspects de la finance.
Coûts et bénéfices : Les fonctions affines peuvent être utilisées pour modéliser les coûts fixes et variables dans la gestion d'une entreprise, ainsi que les revenus et les bénéfices
Cinématique : En physique, les fonctions affines peuvent être utilisées pour décrire le mouvement linéaire en fonction du temps, comme la position d'un objet en mouvement. Lois de Hooke : Les fonctions affines sont utilisées pour modéliser la relation entre la force appliquée et la déformation dans les matériaux élastiques, conformément à la loi de Hooke.
Analyse de structures : Les fonctions affines peuvent être utilisées pour analyser les contraintes et les déformations dans des structures linéaires, comme des poutres ou des ponts.
Régression linéaire : Les fonctions affines sont couramment utilisées pour effectuer des régressions linéaires, ce qui permet de trouver une relation linéaire entre des variables et de prédire des valeurs futures.
Temps de déplacement : Les fonctions affines peuvent être utilisées pour modéliser le temps de déplacement entre deux endroits en fonction de la distance
Programmation linéaire : Les fonctions affines sont utilisées dans la programmation linéaire pour optimiser des problèmes où les relations entre les variables sont linéaires.
Progression académique : Les fonctions affines peuvent être utilisées pour modéliser la progression des élèves en fonction du temps d'étude ou de la pratique.
Conception de bâtiments : Les fonctions affines peuvent être utilisées pour modéliser des dimensions de bâtiments, telles que la hauteur en fonction du nombre d'étages.. |
Erreurs ou confusions éventuelles
Erreur: Croire que
- Intervertir les rôles de la pente (a) et de l'ordonnée à l'origine (b).
- Erreurs dans les calculs mathématiques
- Erreurs d'interprétation des graphiques.
- Oublier la distinction entre le domaine et le codomaine.
- Comprendre l'inversibilité.
- Erreurs de signe.
- Ignorer l'importance de la variable indépendante
- Négliger l'influence de la pente sur la pente et l'inclinaison de la droite.
- Interpréter de manière erronée les intersections.
- Ignorer la possibilité d'une fonction constante
- Sous-estimer l'utilité des fonctions affines.
- Oublier de prendre en compte l'unité de mesure.
- Ignorer les applications dans le monde réel.
Confusion possible ou glissement de sens
- Confusion entre Fonction affine - Fonction linéaire
- Confusion entre Fonction constante - Fonction affine
- Confusion entre Parallèle - Perpendiculaire
- Confusion entre Inéquations linéaires - Equations linéaires
- Confusion entre Fonction affine - Equation de droite
- Confusion entre termes Linéaire - Affine
- Confusion entre Fonctions affines - Fonctions quadratiques
Questions possibles
- Qu'est-ce qu'une fonction affine, et comment est-elle mathématiquement définie?
- Pouvez-vous expliquer la signification des coefficients "a" et "b" dans une fonction affine?
- Comment déterminez-vous la pente d'une fonction affine à partir de son équation?
- Quelle est l'importance de l'ordonnée à l'origine dans une fonction affine?
- Comment identifiez-vous le domaine d'une fonction affine?
- Quelles sont les applications courantes des fonctions affines en économie?
- Comment résolvez-vous une inéquation linéaire impliquant une fonction affine?
- Quelle est la différence entre une fonction affine et une fonction linéaire?
- Pouvez-vous donner un exemple concret d'une fonction affine dans la vie quotidienne?
- Comment effectuez-vous une régression linéaire à l'aide d'une fonction affine?
- Quelles sont les propriétés des droites parallèles et des droites perpendiculaires en termes de fonctions affines?
- Comment pouvez-vous identifier l'intersection de deux fonctions affines?
- Pouvez-vous expliquer comment modéliser une relation linéaire en utilisant une fonction affine?
- Dans une situation donnée, comment déterminez-vous si une relation entre deux variables est mieux représentée par une fonction affine ou une autre forme de fonction mathématique?
- Comment une fonction affine peut-elle être utilisée pour prédire des valeurs futures en fonction de données antérieures?
- Quelle est l'utilité des fonctions affines en géométrie analytique pour décrire des lignes droites?
- Comment une fonction affine est-elle utilisée pour modéliser des coûts dans le domaine de la gestion d'entreprise?
- Comment interprétez-vous graphiquement les paramètres "a" et "b" d'une fonction affine?
- Pouvez-vous résoudre une équation affine pour trouver les valeurs de "x" ou de "f(x)"?
- Comment une fonction affine est-elle utilisée dans la musique pour représenter des progressions d'accords?
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
- Contextualiser les concepts.
- Utiliser des représentations visuelles
- Proposer des exemples variés.
- Encourager l'expérimentation.
- Créer des problèmes concrets.
- Relier à d'autres concepts mathématiques.
- Utiliser la technologie.
- Suivre une progression pédagogique.
- Favoriser les discussions en classe
- Fournir une rétroaction constructive.
- Examiner les erreurs courantes.
- Mettre en avant l'importance des erreurs
Aides et astuces
- Interprétation graphique : Comprenez la signification graphique de la pente (coefficient directeur) et de l'ordonnée à l'origine. La pente représente la pente de la droite, et l'ordonnée à l'origine est l'endroit où la droite coupe l'axe vertical.
- Simplification des expressions : Les fonctions affines sont souvent écrites sous forme générale f(x)=mx+b, mais vous pouvez les simplifier pour des cas particuliers. Par exemple, si b=0, la fonction devient f(x)=mx
- Représentation graphique : Utilisez un graphique pour visualiser la fonction affine. Cela peut vous aider à comprendre son comportement, sa pente, et son intersection avec d'autres fonctions.
- Systèmes d'équations linéaires : Les fonctions affines peuvent être utilisées pour modéliser et résoudre des systèmes d'équations linéaires. Si vous avez plusieurs fonctions affines, représentez-les sous forme d'un système d'équations linéaires pour résoudre simultanément les inconnues.
Education: Autres liens, sites ou portails
Bibliographie
Pour citer cette page: (affine)
ABROUGUI, M & al, 2023. Fonction affine. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Fonction_affine>, consulté le 24, novembre, 2024
- ..................
- ..................
- ..................
- ..................
- Sponsors Education
- Mathématiques (Concepts)
- Économie (Concepts)
- Finance (Concepts)
- Physique (Concepts)
- Ingénierie (Concepts)
- Statistiques (Concepts)
- Informatique (Concepts)
- Gestion (Concepts)
- Géographie (Concepts)
- Chimie (Concepts)
- Biologie (Concepts)
- Psychologie (Concepts)
- Éducation (Concepts)
- Architecture (Concepts)
- Musique (Concepts)
- Fonction affine
- Coefficient directeur (a)
- Ordonnée à l'origine (b)
- Droite affine
- Relation linéaire
- Droite parallèle et droite perpendiculaire
- Intersection de droites
- Inéquations linéaires
- Régression linéaire
- Domaine et codomaine
- Image
- Pente et ordonnée à l'origine
- Parallélisme et perpendicularité
- Racine et zéro de la fonction
- Fonction constante
- Inversibilité
- Variation linéaire
- Concepts
- Fonction affine (Concepts)
- Fiche conceptuelle didactique
