Différences entre versions de « Moyennes »
De Didaquest
Aller à la navigationAller à la recherche| (12 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 62 : | Ligne 62 : | ||
|Typologie= <!------------------------------------ Ne pas Modifier --> | |Typologie= <!------------------------------------ Ne pas Modifier --> | ||
<!-- ****************** Commercez les modifications ****************--> | <!-- ****************** Commercez les modifications ****************--> | ||
| − | * | + | * La [[moyenne arithmétique]] d'un groupe de valeurs exprime la grandeur qu'aurait chaque valeur si elles étaient toutes identiques, sans changer la valeur totale de l'ensemble. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}}<!-- ******** Fin Fiche Didactique Définition ******************* --> | }}<!-- ******** Fin Fiche Didactique Définition ******************* --> | ||
| Ligne 83 : | Ligne 77 : | ||
<!-- Remplacez, Adaptez, Ajoutez ou Supprimez les images et lignes non utilisées--> | <!-- Remplacez, Adaptez, Ajoutez ou Supprimez les images et lignes non utilisées--> | ||
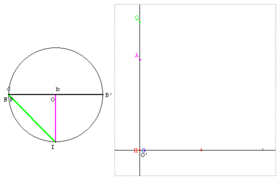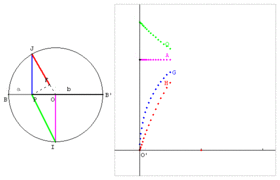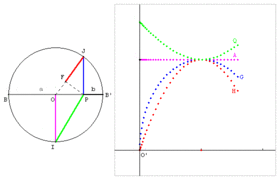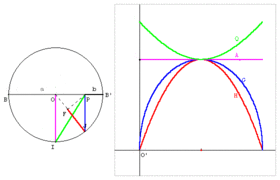
| − | Image: | + | Image:Moyennes-QAGH.gif|Moyenne QAGH : B, B’ et P sont trois points alignés tels que BP = a et B’P = b. Sur le cercle de diamètre BB’ = a + b, soit un point J libre. Le point P est le projeté de J sur [BB’]. Le point F est le projeté de P sur [OJ]. Le point I est un des points du cercle qui se projette en O. - OI est la moyenne arithmétique de a et b. - PJ est la moyenne géométrique de a et b. - FJ est la moyenne harmonique de a et b. - PI est la moyenne quadratique de a et b. |
Image:Definition-graphique-concept2.png|Titre de Votre Image 2 | Image:Definition-graphique-concept2.png|Titre de Votre Image 2 | ||
Image:Definition-graphique-concept3.png|Titre de Votre Image 3 | Image:Definition-graphique-concept3.png|Titre de Votre Image 3 | ||
| Ligne 135 : | Ligne 129 : | ||
* La '''note moyenne''' est la note moyenne totale pour tous les cours suivis aux fins de crédits durant un semestre ou une année. La '''note moyenne cumulative''' est la moyenne pour toutes les notes méritées durant plusieurs semestres ou années à un établissement scolaire. | * La '''note moyenne''' est la note moyenne totale pour tous les cours suivis aux fins de crédits durant un semestre ou une année. La '''note moyenne cumulative''' est la moyenne pour toutes les notes méritées durant plusieurs semestres ou années à un établissement scolaire. | ||
| − | *............. | + | * Croissance bactérienne et moyenne géométrique : http://infos41.pagesperso-orange.fr/SCSE/fichiers%20pdf/TST2Spdf/TP41-Versunefonctionexpo. |
| − | .. | + | * Moyenne quadratique : Cas en biophysique vitesse des gaz (pollution) moyenne quadratique des vitesses d |
| − | .. | + | ’une particule : http://images.math.cnrs.fr/Moyennes-II-la-moyenne-quadratique.html ou moyenne quadratique des vitesses d |
| − | + | ’une particule | |
| + | (exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html) | ||
| + | :* concentrations cellulaires de laits ://idele.fr/presse/publication/idelesolr/recommends/modes-de-calcul-des-moyennes-principes-generaux.html | ||
| + | :* Moyenne Mobile : https://support.minitab.com/fr-fr/minitab/18/help-and-how-to/modeling-statistics/time-series/how-to/moving-average/methods-and-formulas/methods-and-formulas/ | ||
| + | |||
}}<!--************** Fin Fiche Didactique Explicitations ******************* --> | }}<!--************** Fin Fiche Didactique Explicitations ******************* --> | ||
| Ligne 154 : | Ligne 152 : | ||
* Confusion entre: [[Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique]] | * Confusion entre: [[Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique]] | ||
* Choix et pertinences : [[Moyenne - Mode - Médiane]] | * Choix et pertinences : [[Moyenne - Mode - Médiane]] | ||
| + | * [https://lexique.netmath.ca/classe-modale/ Difficulté de calcul du mode dans une classe modale] | ||
| Ligne 204 : | Ligne 203 : | ||
etc... | etc... | ||
| + | * Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). ('''Cadrer''' bien l''''Arc''' pour '''Jouer''' en '''Harmonie''' du plus grand au plus petit => QAGH) | ||
}}<!-- ************************* Fin Astuces-Enseignement ********************** --> | }}<!-- ************************* Fin Astuces-Enseignement ********************** --> | ||
| Ligne 215 : | Ligne 215 : | ||
:* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | :* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | ||
:* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html | :* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html | ||
| − | :* ....... | + | :* Les moyennes non arithmétiques : http://www.jybaudot.fr/Stats/moyennesnonarithm.html |
| − | :* .... | + | :* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html |
| − | + | :* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | |
}}<!-- ************ Fin Liens Education ********************** --> | }}<!-- ************ Fin Liens Education ********************** --> | ||
Version actuelle datée du 2 juillet 2018 à 17:27
 Votre Publicité sur le Réseau
|
Traduction
Traductions
Définition
Domaine, Discipline, Thématique
Justification
Définition écrite
- ......................................................................
....................................................................... ....................................................................... .......................................................................
- ......................................................................
.......................................................................
.......................................................................
|
Moyennes - Historique (+)
Définition graphique
Moyenne QAGH : B, B’ et P sont trois points alignés tels que BP = a et B’P = b. Sur le cercle de diamètre BB’ = a + b, soit un point J libre. Le point P est le projeté de J sur [BB’]. Le point F est le projeté de P sur [OJ]. Le point I est un des points du cercle qui se projette en O. - OI est la moyenne arithmétique de a et b. - PJ est la moyenne géométrique de a et b. - FJ est la moyenne harmonique de a et b. - PI est la moyenne quadratique de a et b.
Titre de Votre Image 2
Titre de Votre Image 3
{{{AutresMedias}}}
Concepts ou notions associés
Moyennes - Glossaire / (+)
Exemples, applications, utilisations
’une particule : http://images.math.cnrs.fr/Moyennes-II-la-moyenne-quadratique.html ou moyenne quadratique des vitesses d ’une particule (exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html)
|
Erreurs ou confusions éventuelles
Questions possibles
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
- Expliquer le calcul de chaque type de moyenne ou expliquer le choix de l'une en fonction de la situation ?
Aides et astuces
- il existe des moyennes quadratiques, harmoniques, géométriques et aussi arithmétique. L'usage de l'une plutôt que l'autre dépend du rôle que l'on veut faire jouer à la moyenne.
- Si elle intervient comme diviseur (cas de la vitesse, mais aussi d'un indice de prix qui servira à éliminer l'inflation) il vaut mieux prendre une moyenne harmonique
- Si elle intervient comme un carré (la tension en électicité, le rayon d'un cercle dont la surface nous intéresse..) il vaut mieux une moyenne quadratique.
- Si elle intervient comme facteur multiplicatif, ce sera géométrique
etc...
- Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). (Cadrer bien l'Arc pour Jouer en Harmonie du plus grand au plus petit => QAGH)
Education: Autres liens, sites ou portails
- http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm
- http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html
- Les moyennes non arithmétiques : http://www.jybaudot.fr/Stats/moyennesnonarithm.html
- http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html
- http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm
Bibliographie
Pour citer cette page: ([1])
ABROUGUI, M & al, 2018. Moyennes. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Moyennes>, consulté le 21, novembre, 2024
- https://www.khanacademy.org/math/ap-statistics/summarizing-quantitative-data-ap/measuring-center-quantitative/v/statistics-intro-mean-median-and-mode
- http://images.math.cnrs.fr/Moyennes-I.html
- http://images.math.cnrs.fr/Moyennes-II.html
- http://images.math.cnrs.fr/Moyennes-III.html
- https://www.stem.org.uk/resources/community/collection/22442/mean-mode-and-median
- https://www.jic.ac.uk/services/statistics/readingadvice/booklets/topbak.html
