Mitose2

Autres Fiches Conceptuelles

Posez une Question

(+)

Votre Publicité sur le Réseau

Traduction

Mitose2 (Français) mitose / Concept en Anglais (Anglais)mitosis / Concept en Arabe (Arabe)الانقسام المتساوي

(+)

Traductions

Définition

Domaine, Discipline, Thématique

(+)

.génétique / biotechnologie / biologie cellulaire / cytologie / biologie animale / biologie végétale / médecine / histologie / évolution /

Justification

Définition écrite

• nom féminin

grec (mitos -filament) la mitose correspond a l’étape de la division cellulaire chez les cellules non sexuelles des organismes eucaryotes (c'est a dire qui possèdent un noyau). elle se déroule en plusieurs phases, commence après la duplication de l'ADN et se termine avec la séparation égale des deux cellules filles. synonyme = caryocinèse elle comprend quatre phase pendant lesquelles l'information génétique des chromosomes va se repartir exactement entre les deux nouvelles cellules.

Reproduction cyclique et non sexuée qui s'effectue par une division cellulaire au sein d'un organisme pour qu'il se développe

Exemple : La mitose est l’une des étapes les plus importantes du cycle de reproduction cellulaire. i** Fin Définition Générale ***************************** -->

(+)

...................................................................... ....................................................................... ....................................................................... ....................................................................... ...................................................................... ....................................................................... .......................................................................

Mitose2 - Historique (+)

Définition graphique

• 

  Mitose phases

• 

  mitose2

• 

  phase de mitose 2

• 

  erreur de positionnement

{{{AutresMedias}}}

Concepts ou notions associés

(+)

anaphase / culture in vitro / mutation / reproduction conforme / physiologie végétale / télophase / métaphase / biologie /

Mitose2 - Glossaire / (+)

Exemples, applications, utilisations

la mitose est utilisée dans le domaine agricole pour réaliser: le clonage des végétaux par le biais de la multiplication végétative traditionnelle et la cultures invitro. le clonage des animaux qui consiste à transférer le noyau de cellule somatique. En effet, Une copie génétique d’un animal est produite en remplaçant le noyau d’un ovule non fécondé (cellule-œuf) par celui d’une cellule du corps (cellule somatique) de l’animal pour former un embryon. L’embryon est ensuite transféré dans l’utérus d’une mère porteuse, où il se développe alors jusqu’à la naissance. (+)

a mitose est utilisée dans le domaine agricole pour réaliser:

Erreurs ou confusions éventuelles

• Confusion entre mitose - méiose
• Confusion entre mitose - amitose
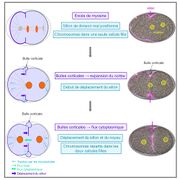
• Erreur fréquente: de répartition du matériel génétique

Les erreurs de répartition du matériel génétique lors de la division cellulaire peuvent avoir des conséquences dramatiques sur la vie des cellules-filles. Dans une étude publiée dans la revue Current Biology, les chercheurs révèlent l’existence d’un mécanisme de correction des erreurs de répartition de l’ADN inédit dans lequel les changements de tension cellulaire jouent un rôle essentiel.

Lorsque cellule se divise, son matériel génétique doit être réparti équitablement entre ses deux cellules-filles. Cette ségrégation du matériel génétique est une caractéristique essentielle de la division cellulaire. En effet, une mauvaise répartition de l’ADN provoque une aneuploïdie des deux cellules-filles qui peut conduire à leur transformation tumorale.

(+)

Questions possibles

https://rnbio.upmc.fr/bio-cell_mitose_question1

https://rnbio.upmc.fr/bio-cell_mitose_question2 https://rnbio.upmc.fr/bio-cell_mitose_question3 https://rnbio.upmc.fr/bio-cell_mitose_question6 https://rnbio.upmc.fr/bio-cell_mitose_question7 https://rnbio.upmc.fr/bio-cell_mitose_question8 https://rnbio.upmc.fr/bio-cell_mitose_question9 https://rnbio.sorbonne-universite.fr/bio-cell_mitose_question6 https://rnbio.sorbonne-universite.fr/bio-cell_mitose_question7 https://rnbio.sorbonne-universite.fr/bio-cell_mitose_question8 https://rnbio.sorbonne-universite.fr/bio-cell_mitose_question9

(+)

Liaisons enseignements et programmes

Idées ou Réflexions liées à son enseignement

• idées liées à son enseignement

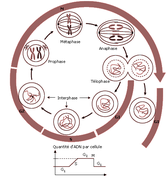
- Observer des cellules en division dans des zones spécialisées localisées à l’extrémité des tiges ou des racines, appelées méristèmes, assurent la production de nouvelles cellules et par conséquent la croissance en longueur de ces organes. - Exploiter des électronographies des différentes phases de mitose ainsi que leurs schémas d’interprétation - Utiliser des fonds de schémas pour représenter le comportement des chromosomes au cours des différentes phases de la mitose - Exploiter des animations qui simulent le phénomène de la mitose - Insister sur les phases déterminantes qui permettent la conservation du nombre de chromosomes entre la cellule mère et les cellules filles - Analyser les courbes de la répartition de la quantité d’ADN au cours des différentes phases de la mitose et décrire en parallèle le comportement des chromosomes

(+)

Aides et astuces

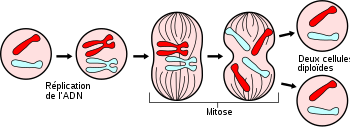
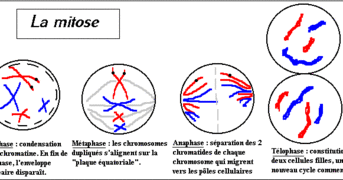
• 1) Prophase : L'enveloppe nucléaire se décompose, les composants du noyau se dispersent dans le cytoplasme.

2) Métaphase : C'est la duplication des chromosomes.

3) Anaphase : Les chromatides se séparent et mirent vers les pôles opposés à la cellule.

4) Télophase : Une enveloppe nucléaire se forme autour de chaque lot de chromosomes.

Astuce mnémotechnique :

Papa Maman A Table = Prophase Métaphase Anaphase Télophase

Education: Autres liens, sites ou portails

https://cmapscloud.ihmc.us/rid=1XH3GV0GF-208NPM9-5X6TD2

• .................
• ..................

Bibliographie

Pour citer cette page: ([1])

ABROUGUI, M & al, 2022. Mitose2. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Mitose2>, consulté le 28, décembre, 2024

• ..................
• ..................
• ..................
• ..................

Donnez votre avis sur les fiches conceptuelles