Différences entre versions de « Moyennes »
| (8 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 62 : | Ligne 62 : | ||
|Typologie= <!------------------------------------ Ne pas Modifier --> | |Typologie= <!------------------------------------ Ne pas Modifier --> | ||
<!-- ****************** Commercez les modifications ****************--> | <!-- ****************** Commercez les modifications ****************--> | ||
| − | * | + | * La [[moyenne arithmétique]] d'un groupe de valeurs exprime la grandeur qu'aurait chaque valeur si elles étaient toutes identiques, sans changer la valeur totale de l'ensemble. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}}<!-- ******** Fin Fiche Didactique Définition ******************* --> | }}<!-- ******** Fin Fiche Didactique Définition ******************* --> | ||
| Ligne 83 : | Ligne 77 : | ||
<!-- Remplacez, Adaptez, Ajoutez ou Supprimez les images et lignes non utilisées--> | <!-- Remplacez, Adaptez, Ajoutez ou Supprimez les images et lignes non utilisées--> | ||
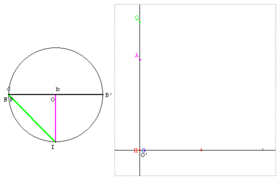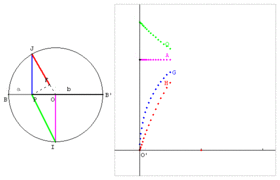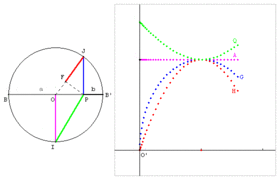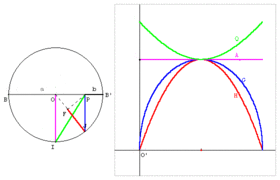
| − | Image: | + | Image:Moyennes-QAGH.gif|Moyenne QAGH : B, B’ et P sont trois points alignés tels que BP = a et B’P = b. Sur le cercle de diamètre BB’ = a + b, soit un point J libre. Le point P est le projeté de J sur [BB’]. Le point F est le projeté de P sur [OJ]. Le point I est un des points du cercle qui se projette en O. - OI est la moyenne arithmétique de a et b. - PJ est la moyenne géométrique de a et b. - FJ est la moyenne harmonique de a et b. - PI est la moyenne quadratique de a et b. |
Image:Definition-graphique-concept2.png|Titre de Votre Image 2 | Image:Definition-graphique-concept2.png|Titre de Votre Image 2 | ||
Image:Definition-graphique-concept3.png|Titre de Votre Image 3 | Image:Definition-graphique-concept3.png|Titre de Votre Image 3 | ||
| Ligne 140 : | Ligne 134 : | ||
’une particule | ’une particule | ||
(exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html) | (exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html) | ||
| + | :* concentrations cellulaires de laits ://idele.fr/presse/publication/idelesolr/recommends/modes-de-calcul-des-moyennes-principes-generaux.html | ||
| + | :* Moyenne Mobile : https://support.minitab.com/fr-fr/minitab/18/help-and-how-to/modeling-statistics/time-series/how-to/moving-average/methods-and-formulas/methods-and-formulas/ | ||
}}<!--************** Fin Fiche Didactique Explicitations ******************* --> | }}<!--************** Fin Fiche Didactique Explicitations ******************* --> | ||
| Ligne 156 : | Ligne 152 : | ||
* Confusion entre: [[Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique]] | * Confusion entre: [[Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique]] | ||
* Choix et pertinences : [[Moyenne - Mode - Médiane]] | * Choix et pertinences : [[Moyenne - Mode - Médiane]] | ||
| + | * [https://lexique.netmath.ca/classe-modale/ Difficulté de calcul du mode dans une classe modale] | ||
| Ligne 206 : | Ligne 203 : | ||
etc... | etc... | ||
| − | * Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). (Cadrer bien l'Arc pour | + | * Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). ('''Cadrer''' bien l''''Arc''' pour '''Jouer''' en '''Harmonie''' du plus grand au plus petit => QAGH) |
}}<!-- ************************* Fin Astuces-Enseignement ********************** --> | }}<!-- ************************* Fin Astuces-Enseignement ********************** --> | ||
| Ligne 218 : | Ligne 215 : | ||
:* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | :* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | ||
:* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html | :* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html | ||
| − | :* ....... | + | :* Les moyennes non arithmétiques : http://www.jybaudot.fr/Stats/moyennesnonarithm.html |
| − | :* .... | + | :* http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html |
| − | + | :* http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm | |
}}<!-- ************ Fin Liens Education ********************** --> | }}<!-- ************ Fin Liens Education ********************** --> | ||
Version actuelle datée du 2 juillet 2018 à 17:27
 Traduction
Traduction
 Définition
Définition
Domaine, Discipline, Thématique
Définition écrite
- ......................................................................
....................................................................... ....................................................................... .......................................................................
- ......................................................................
.......................................................................
.......................................................................
|
Définition graphique
Moyenne QAGH : B, B’ et P sont trois points alignés tels que BP = a et B’P = b. Sur le cercle de diamètre BB’ = a + b, soit un point J libre. Le point P est le projeté de J sur [BB’]. Le point F est le projeté de P sur [OJ]. Le point I est un des points du cercle qui se projette en O. - OI est la moyenne arithmétique de a et b. - PJ est la moyenne géométrique de a et b. - FJ est la moyenne harmonique de a et b. - PI est la moyenne quadratique de a et b.
 Concepts ou notions associés
Concepts ou notions associés
 Exemples, applications, utilisations
Exemples, applications, utilisations
’une particule : http://images.math.cnrs.fr/Moyennes-II-la-moyenne-quadratique.html ou moyenne quadratique des vitesses d ’une particule (exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html)
|
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
 Questions possibles
Questions possibles
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
- Expliquer le calcul de chaque type de moyenne ou expliquer le choix de l'une en fonction de la situation ?
Aides et astuces
- il existe des moyennes quadratiques, harmoniques, géométriques et aussi arithmétique. L'usage de l'une plutôt que l'autre dépend du rôle que l'on veut faire jouer à la moyenne.
- Si elle intervient comme diviseur (cas de la vitesse, mais aussi d'un indice de prix qui servira à éliminer l'inflation) il vaut mieux prendre une moyenne harmonique
- Si elle intervient comme un carré (la tension en électicité, le rayon d'un cercle dont la surface nous intéresse..) il vaut mieux une moyenne quadratique.
- Si elle intervient comme facteur multiplicatif, ce sera géométrique
etc...
- Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). (Cadrer bien l'Arc pour Jouer en Harmonie du plus grand au plus petit => QAGH)
Education: Autres liens, sites ou portails
- http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm
- http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html
- Les moyennes non arithmétiques : http://www.jybaudot.fr/Stats/moyennesnonarithm.html
- http://www.irem.univ-mrs.fr/Moyennes-arithmetique-geometrique,277.html
- http://villemin.gerard.free.fr/aMaths/Moyenne/Comparai.htm
 Bibliographie
Bibliographie
Pour citer cette page: ([1])
ABROUGUI, M & al, 2018. Moyennes. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Moyennes>, consulté le 21, novembre, 2024
- https://www.khanacademy.org/math/ap-statistics/summarizing-quantitative-data-ap/measuring-center-quantitative/v/statistics-intro-mean-median-and-mode
- http://images.math.cnrs.fr/Moyennes-I.html
- http://images.math.cnrs.fr/Moyennes-II.html
- http://images.math.cnrs.fr/Moyennes-III.html
- https://www.stem.org.uk/resources/community/collection/22442/mean-mode-and-median
- https://www.jic.ac.uk/services/statistics/readingadvice/booklets/topbak.html