Moyennes
 Votre Publicité sur le Réseau
|
Traduction
Traductions
Définition
Domaine, Discipline, Thématique
Justification
Définition écrite
- ......................................................................
....................................................................... ....................................................................... .......................................................................
- ......................................................................
.......................................................................
.......................................................................
....................................................................... ....................................................................... .......................................................................
....................................................................... ....................................................................... |
Moyennes - Historique (+)
Définition graphique
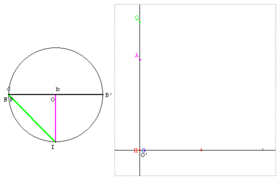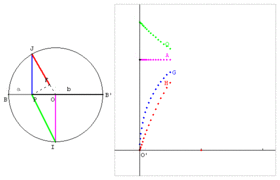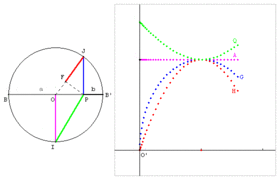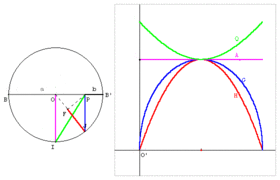
Moyenne QAGH : B, B’ et P sont trois points alignés tels que BP = a et B’P = b. Sur le cercle de diamètre BB’ = a + b, soit un point J libre. Le point P est le projeté de J sur [BB’]. Le point F est le projeté de P sur [OJ]. Le point I est un des points du cercle qui se projette en O. - OI est la moyenne arithmétique de a et b. - PJ est la moyenne géométrique de a et b. - FJ est la moyenne harmonique de a et b. - PI est la moyenne quadratique de a et b.
Titre de Votre Image 2
Titre de Votre Image 3
{{{AutresMedias}}}
Concepts ou notions associés
Moyennes - Glossaire / (+)
Exemples, applications, utilisations
’une particule : http://images.math.cnrs.fr/Moyennes-II-la-moyenne-quadratique.html ou moyenne quadratique des vitesses d ’une particule (exercice : http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_05.html ou http://res-nlp.univ-lemans.fr/NLP_E_M10_G02/co/NLP_E_M10_G02_08.html) |
Erreurs ou confusions éventuelles
- Généralisation abusive : Moyenne - Moyenne Arithmétique
- Confusion entre: Moyennes: Arithmétique - Géométrique - Harmonique - Quadratique
- Choix et pertinences : Moyenne - Mode - Médiane
Questions possibles
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
- Expliquer le calcul de chaque type de moyenne ou expliquer le choix de l'une en fonction de la situation ?
Aides et astuces
- il existe des moyennes quadratiques, harmoniques, géométriques et aussi arithmétique. L'usage de l'une plutôt que l'autre dépend du rôle que l'on veut faire jouer à la moyenne.
- Si elle intervient comme diviseur (cas de la vitesse, mais aussi d'un indice de prix qui servira à éliminer l'inflation) il vaut mieux prendre une moyenne harmonique
- Si elle intervient comme un carré (la tension en électicité, le rayon d'un cercle dont la surface nous intéresse..) il vaut mieux une moyenne quadratique.
- Si elle intervient comme facteur multiplicatif, ce sera géométrique
etc...
- Sur un même échantillon la moyenne la plus élevée est la quadratique, suivie de l'arithmétique, la géométrique et enfin l'harmonique (avec xi > 0). (Cadrer bien l'Arc pour tirer en Harmonie du plus grand au plus petit => QAGH)
Education: Autres liens, sites ou portails
Bibliographie
Pour citer cette page: ([1])
ABROUGUI, M & al, 2018. Moyennes. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Moyennes>, consulté le 24, novembre, 2024
- https://www.khanacademy.org/math/ap-statistics/summarizing-quantitative-data-ap/measuring-center-quantitative/v/statistics-intro-mean-median-and-mode
- http://images.math.cnrs.fr/Moyennes-I.html
- http://images.math.cnrs.fr/Moyennes-II.html
- http://images.math.cnrs.fr/Moyennes-III.html
- https://www.stem.org.uk/resources/community/collection/22442/mean-mode-and-median
- https://www.jic.ac.uk/services/statistics/readingadvice/booklets/topbak.html
