Ecriture et représentation vectorielles
 Traduction
Traduction
Ecriture et représentation vectorielles (Français) / Vectorial writing and representation (Anglais) / كتابة القيمة المتجهة و تمثيلها (Arabe)
 Définition
Définition
- Domaine, Discipline, Thématique :
Catégorie: Algèbre / Catégorie: Géométrie / Catégorie: Physique
Définition écrite
un vecteur est un objet généralisant plusieurs notions provenant de la géométrie (couples de points, translations, etc.), de l'algèbre (« solution » d'un système d'équations à plusieurs inconnues), ou de la physique (forces, vitesses, accélérations, etc.)
Pour nos besoins (la physique du lycée et des classes prépas), on va en rester à la définition élémentaire. On définit le vecteur AB, que je note en gras selon la convention typographique des physiciens, comme un objet possédant: une direction: le bipoint (A,B) s'appuie sur une droite support, un sens: le bipoint est orienté. A est son origine et B son extrémité, un point d'application, qui sera A. C'est ici que notre définition est élémentaire. Ceux que ça intéresse creuseront et tomberont sur les classes d'équivalence, les vecteurs liés, les glisseurs, etc. une norme, qui est définie comme la distance euclidienne entre A et B. On la note ||AB|| ou plus simplement AB = ||AB||. En physique, on parle aussi d'intensité ou de module. Attention, il existe une différence formelle entre la notion de norme de vecteur en mathématique et d'intensité (ou module) en physique : une norme au sens mathématique ne possède pas d'unité, alors que l'intensité en physique en possède une (une force s'exprime en newton par exemple). Dans la vie courante, peu de gens font la distinction.... La norme d'un vecteur est un réel toujours positif ou nul. Un vecteur dont la norme est égale à 1 est dit "unitaire". |
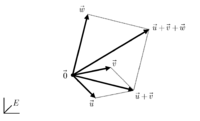
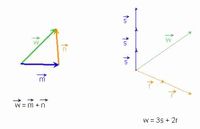
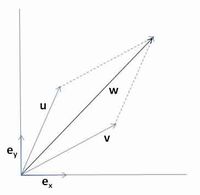
Définition graphique
 Concepts ou notions associés
Concepts ou notions associés
 Exemples, applications, utilisations
Exemples, applications, utilisations
- Force résultante
- Champ résultant
- Repère
- Représentation des grandeurs vectorielles
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
- La physique est à l'origine du terme de vecteur, elle utilise toujours largement ce concept. La raison historique provient du fait qu'en physique classique l'espace qui nous entoure est bien modélisé comme espace affine (géométrie euclidienne) de dimension trois avec le temps (absolu) comme paramètre d'évolution. En physique, une addition de vecteurs ne peut avoir de sens que si leurs coordonnées respectives ont la même dimension.
- Soit un vecteur u et un réel k. Le produit du réel k et du vecteur u donne un vecteur ku qui possède les propriétés suivantes:
il possède la même direction que u. son sens dépend du signe de k : si k > 0 alors u et ku ont le même sens. Si k < 0, ils sont de sens opposé. ||ku|| = k||u|| la multiplication d'un vecteur par un scalaire est associative, distributive et admet un élément neutre (k=1)
 Questions possibles
Questions possibles
- Comment déterminer le vecteur champ résultant ou la force résultante?
- Comment représenter ou modéliser une grandeur vectorielle ( champ, force,..)
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
- Portail Formation Gratuite
- Multisites Educatifs
- Sur DidaQuest
- Sur le Portail Didactique.info
- Sur le Portail Questions / Réponses
- Concept Sur Wikipedia
- Concept Sur Wikiwand
- Concept Sur Wikiversity
 Aides, Astuces,...
Aides, Astuces,...
Soit u un vecteur quelconque. On appelle composantes du vecteur u le triplet (je considère que je suis dans R3) de réels (x, y, z) tel que u = x*ex + y*ey + z*ez.
Voyons ce que cela donne pour un vecteur AB dans le plan euclidien muni d'un repère (O, ex , ey , ez). Comment calculer ses composantes, problème bien classique en physique? Il suffit de remarquer que:
OA = xa*ex + ya*ey + za*ez
OB = xb*ex + yb*ey + zb*ez
et donc AB = AO + OB = OB - OA = (xb - xa)*ex + (yb - ya)*ey + (zb - za)*ez
La norme du vecteur u (son carré en l'occurrence) est donnée par la formule, à connaitre par coeur : ||AB||2 = (xb - xa)2 + (yb - ya)2 + (zb - za)2
Multiplication par un scalaire
Soit un vecteur u et un réel k. Le produit du réel k et du vecteur u donne un vecteur ku qui possède les propriétés suivantes:
il possède la même direction que u. son sens dépend du signe de k : si k > 0 alors u et ku ont le même sens. Si k < 0, ils sont de sens opposé. ||ku|| = k||u|| la multiplication d'un vecteur par un scalaire est associative, distributive et admet un élément neutre (k=1) Le produit scalaire de deux vecteurs u et v est un nombre réel (on dit aussi scalaire) défini comme le produit de leur norme et du cosinus de l'angle que forme les deux vecteurs:
u.v = ||u||*||v||*cos(u,v)
Notez la manière d'écrire le produit scalaire avec un point.
Le produit scalaire peut donc être positif ou négatif selon la valeur de l'angle. Très important, il est nul lorsque u et v sont orthogonaux, propriété à connaitre par coeur.
Quelques propriétés du produit scalaire:
il est commutatif u.v = v.u il est bilinéaire : (u + v).w = u.w + u.w et (m.u).(nv) = (m*n)(u.v) Soient (x1,y1,z1) les composantes du vecteur u et (x2,y2,z2) les composantes du vecteur v dans un repère orthonormé, le produit scalaire est défini par
u.v = x1*x2 + y1*y2 + z1*z2
Trois remarques importantes:
D'après cette définition et la définition de la norme d'un vecteur donnée ci-dessus, on a donc ||u||² = u.u Si A est un vecteur quelconque sur une droite, le vecteur i = A/||A|| est le vecteur unitaire fixant la direction de A. Le produit scalaire et la norme sont des invariants par translation et par rotation du repère et ils ne dépendent pas non plus de son orientation. Enfin, savez-vous que le produit scalaire permet de retrouver le théorème d'Al-Kashi en deux lignes de calcul....
=
 Difficultés liées à son enseignement =
Difficultés liées à son enseignement =
- Balayage entre aspect physique et aspect mathématique
* Balayage entre registre formel( écriture analytique) et registre graphique( représentation graphique)
 Liens Internet
Liens Internet
- URL :
- URL :