Soustraction

Autres Fiches Conceptuelles

Posez une Question

(+)

Votre Publicité sur le Réseau

Traduction

La soustraction (Français) / Subtraction (Anglais) / الطرح (Arabe) / Sustracción (Espagnol) / Subtração (Portugais) / Вычитание (Russe) / Sottrazione (Italien) / Subtraktion (Allemand) / 减法 (Chinois) / घटाव (Hindi) / 減法 (Japonais) / বিয়োগ (Bengali)

(+)

Traductions

Définition

Domaine, Discipline, Thématique

(+)

Mathématiques / Éducation / Informatique / Sciences économiques / Gestion / Physique / Ingénierie / Psychologie cognitive / Pédagogie / Didactique /

Justification

Définition écrite

• La Modèle:Soustraction est une Modèle:Opération mathématique qui consiste à retirer une quantité d'une autre, permettant de trouver la Modèle:Différence entre les deux.
• Elle est représentée par le signe Modèle:− et est l'inverse de Modèle:L'addition.
• La Modèle:Soustraction est essentielle dans divers domaines tels que les Modèle:Finances, les Modèle:Sciences et les Modèle:Applications pratiques quotidiennes (calculs de distances, de temps, de poids, etc.).

(+)

La Modèle:Soustraction peut être effectuée avec différents types de nombres : Modèle:Entiers, Modèle:Fractions, Modèle:Décimales, et Modèle:Nombres négatifs. La méthode classique de soustraction est l'Modèle:Algorithme en colonne, mais d'autres approches existent, comme la soustraction avec des Modèle:Nombres à virgule flottante. En Modèle:Géométrie, la soustraction est utilisée pour calculer les différences de Modèle:Longueurs, Modèle:Aires, ou de Modèle:Volumes. En Modèle:Finance, elle permet de déterminer les Modèle:Pertes, les Modèle:Réductions ou les Modèle:Ajustements de soldes (par exemple, dans le calcul des Modèle:Bilans financiers). La Modèle:Soustraction est également utilisée dans des Modèle:Contextes quotidiens, comme la gestion du Modèle:Temps, la mesure de la Modèle:Distance, et d'autres Modèle:Applications pratiques.

Soustraction - Historique (+)

Définition graphique

• 

  Soustraction

• 

  carte conceptuelle de la soustraction

• 

  Soustraction 1

• AUTRES MEDIAS

Soustraction (Discipline)
Soustraction: (Discipline)
Soustraction: (Discipline)
Soustraction: (Discipline)
Soustraction: (Discipline)
Soustraction
Soustraction
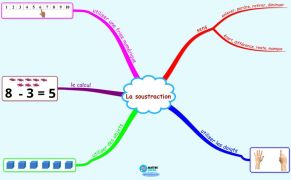
Représentation graphique spatiale carte conceptuelle (cmap)
Document PDF Soustraction: Document PDF
Image/Figure Soustraction: Titre de l'image ou de la figure

Concepts ou notions associés

(+)

Soustraction - Glossaire / (+)

Exemples, applications, utilisations

............................................................................... ................................................................................ ................................................................................ ................................................................................ ............................................................................... ................................................................................ ................................................................................ ................................................................................ (+)

Erreurs ou confusions éventuelles

Exemples de difficultés de compréhension ou d'interprétation courantes:

• Confusion entre soustraction et addition:

Les élèves confondent parfois les signes - et +, surtout lorsqu’ils passent rapidement d’un exercice à l’autre, ce qui entraîne des erreurs dans les calculs.

• Difficulté à comprendre le concept de retenue:

Lorsqu'il s'agit de soustraire un chiffre plus grand d'un plus petit dans une colonne, certains élèves ont du mal à appliquer correctement le concept de retenue, car ils n’ont pas encore pleinement intégré l’idée de "prêt" d’une autre colonne.

• Erreur de placement des chiffres:

Il est fréquent que les élèves alignent mal les chiffres des unités, dizaines et centaines, ce qui fausse leurs calculs.

• Interprétation des zéros dans les soustractions:

Les zéros dans des nombres comme 304 - 27 posent problème, car les élèves ne savent pas comment traiter un zéro lorsqu’il est en haut dans une colonne.

• Incapacité à vérifier les résultats:

Les élèves oublient souvent de vérifier leurs réponses en additionnant le résultat avec le nombre soustrait pour retrouver le total initial.

Confusions ou glissement de sens potentiels

• Retenue - Emprunt :

Certains élèves appellent la retenue un emprunt et n’en comprennent pas le fonctionnement, croyant à tort qu’ils doivent "emprunter" un chiffre d’une autre colonne sans rendre celui qui a été pris. Cela les empêche de comprendre que la retenue modifie temporairement les valeurs des colonnes.

• Valeur positionnelle - Alignement des colonnes :

La confusion entre la valeur positionnelle des chiffres (unités, dizaines, centaines) et l'alignement correct des colonnes lors de la soustraction entraîne des erreurs comme additionner ou soustraire des dizaines à la place des unités.

• Soustraction directe - Résolution par complément :

Lorsque les élèves apprennent différentes stratégies pour résoudre les soustractions (soustraction directe ou complément), certains confondent les étapes et mélangent les deux méthodes, ce qui rend leurs calculs incohérents.

• Zéro dans le minuend - Zéro dans le résultat :

Un zéro dans une soustraction, comme dans 103 - 57, peut entraîner deux confusions : les élèves peuvent croire qu'un zéro indique "rien à soustraire" ou ne pas savoir comment gérer un zéro dans la colonne supérieure (le minuend).

Autres erreurs fréquentes:

• Soustraction horizontale - Soustraction verticale :

Les élèves qui maîtrisent les calculs horizontaux (par exemple, 45 - 23 =) peuvent être désorientés par le passage aux calculs verticaux. La mise en colonne nécessite une compréhension plus fine des valeurs positionnelles, ce qui peut entraîner des erreurs si ce lien n’est pas clair.

• Soustraction avec retenue - Soustraction sans retenue :

Lorsqu’ils rencontrent des soustractions sans retenue, les élèves les trouvent simples et rapides. Cependant, lorsque la retenue est introduite, ils peuvent hésiter ou appliquer la règle de manière incorrecte à toutes les soustractions, même lorsque cela n'est pas nécessaire.

• Soustraction dans un contexte concret - Soustraction dans un contexte abstrait :

Les élèves comprennent souvent mieux la soustraction lorsqu’elle est liée à un problème concret, comme "J'ai 10 bonbons, j'en donne 4". Dans un contexte purement numérique ou abstrait, certains perdent leur repère et ont plus de mal à visualiser l’opération.

• Soustraction - Inversion des termes :

Certains élèves inversent les termes dans une soustraction, par exemple, transformant 52 - 19 en 19 - 52, parce qu'ils pensent que l'ordre n'a pas d'importance comme dans l'addition. Cela peut aboutir à des résultats négatifs, qu'ils ne comprennent pas à leur niveau.

• Utilisation des doigts - Résolution mentale :

La transition entre des stratégies de comptage physique (sur les doigts) et des calculs mentaux est parfois confuse. Les élèves peuvent mélanger les deux méthodes et obtenir des résultats erronés en ne les appliquant pas de manière cohérente.

• Soustraction - Division simplifiée :

Dans des exercices multi-opérations, certains élèves peuvent confondre la soustraction avec une forme de division simplifiée, surtout si les termes semblent liés, comme dans 12 - 6 (parce que 6 est la moitié de 12).

• Zéro comme point de départ - Zéro comme résultat :

Le rôle du zéro dans une soustraction peut être source de confusion. Par exemple, 10 - 10 = 0 peut être interprété à tort comme "il n'y a pas de réponse" ou "l’opération n’a pas de sens", car le concept de "rien" peut être abstrait pour des enfants.

• Soustraction répétée - Division :

Lorsqu’ils effectuent plusieurs soustractions répétées, certains élèves établissent un lien incorrect avec la division sans en comprendre les fondements, par exemple en pensant que 15 - 5 - 5 - 5 = 3 est équivalent à 15 ÷ 5.

• Inattention aux unités :

Dans des problèmes comportant des unités (comme kg, m, €), les élèves oublient souvent d'associer le résultat à l’unité, ce qui peut rendre leur réponse incomplète ou incorrecte, surtout dans des contextes pratiques.

(+)

Questions possibles

• ..................?
• ..................?
• ..................?

(+)

Liaisons enseignements et programmes

Idées ou Réflexions liées à son enseignement

• ..................

• .................

• ..................

• .................

(+)

Education: Autres liens, sites ou portails

Soustraction - Formation/Apprentissage: Exemples de plans structurés (+)

Ressources éducatives et académiques

 Soustraction
 Soustraction
 Soustraction
 Soustraction
 Soustraction
 Soustraction
 Soustraction
 Soustraction
 Soustraction

Autres ressources

• ..................
• ..................
• ..................

Bibliographie

Pour citer cette page: ([1])

ABROUGUI, M & al, 2024. Soustraction. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Soustraction>, consulté le 18, décembre, 2024

• ..................
• ..................
• ..................
• ..................

Donnez votre avis sur les fiches conceptuelles