Les triangles
 Traduction
Traduction
Les triangles (Français)
- Triangle (anglais)
The triangle is a three-sided polygon.
- مثلث (العربية)
المثلث شكل هندسي متكون من ثلاثة اضلاع
 Définition
Définition
Domaine, Discipline, Thématique
Définition écrite
Un triangle est une figure géométrique plane qui se compose de trois points appelés sommets, reliés par trois segments de droite appelés côtés. Voici une définition détaillée d'un triangle en tenant compte des concepts précédemment discutés :
- Sommets (Vertices) : Un triangle a exactement trois sommets, qui sont des points où deux côtés se rencontrent. Les sommets sont généralement étiquetés par des lettres majuscules A, B et C.
- Côtés (Sides) : Un triangle est défini par ses trois côtés, qui sont les segments de droite reliant les sommets. Les côtés sont généralement étiquetés par les lettres minuscules a, b et c. Le côté opposé au sommet A est généralement appelé "côté a", le côté opposé au sommet B est appelé "côté b", et le côté opposé au sommet C est appelé "côté c".
- Angles (Angles) : Chaque sommet d'un triangle forme un angle. Les angles sont généralement étiquetés en utilisant des lettres grecques, telles que α (alpha) pour l'angle au sommet A, β (bêta) pour l'angle au sommet B, et γ (gamma) pour l'angle au sommet C.
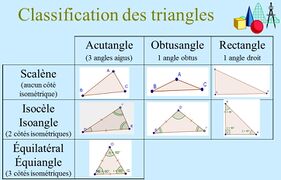
- Types de triangles (Types of Triangles) : Les triangles peuvent être classés en fonction de leurs côtés et de leurs angles :
- Triangle équilatéral : Les trois côtés et les trois angles sont égaux.
- Triangle isocèle : Deux côtés et deux angles sont égaux.
- Triangle scalène : Les trois côtés et les trois angles sont tous différents.
- Triangle rectangle : L'un des angles est un angle droit (90 degrés).
- Propriétés (Properties) : Les triangles ont des propriétés géométriques importantes, notamment le théorème de Pythagore pour les triangles rectangles, les théorèmes des médianes et des bissectrices, les règles de l'inégalité triangulaire, et les lois des sinus et des cosinus pour les triangles quelconques.
- Calcul de l'aire (Area Calculation) : L'aire d'un triangle peut être calculée de plusieurs manières, notamment en utilisant la formule de base x hauteur / 2, la formule d'Héron pour les triangles quelconques, ou en utilisant la trigonométrie pour les triangles rectangles.
- Applications (Applications) : Les triangles sont largement utilisés dans de nombreux domaines, notamment les mathématiques, la géométrie, la trigonométrie, la physique, l'ingénierie, la cartographie, l'art, l'architecture, et bien d'autres.
Un triangle est une figure géométrique constituée de trois sommets reliés par trois côtés, avec des propriétés et des classifications basées sur les longueurs de ses côtés et les mesures de ses angles. Les triangles ont une grande importance dans de nombreuses disciplines et sont étudiés en détail pour comprendre leurs propriétés et leurs applications.
|
En mathématiques, les triangles sont des figures géométriques composées de trois côtés et trois angles. Ils sont l'un des polygones les plus simples mais aussi les plus fondamentaux. Voici quelques concepts clés liés aux triangles en mathématiques :
Triangle Équilatéral : Un triangle ayant tous ses côtés de même longueur. Triangle Isocèle : Un triangle avec au moins deux côtés de même longueur. Triangle Scalène : Un triangle dont tous les côtés ont des longueurs différentes.
La somme des trois angles intérieurs d'un triangle est toujours égale à 180degrés (Théorème des angles d'un triangle). Chaque angle extérieur d'un triangle est égal à la somme des deux angles intérieurs non adjacents.
Un triangle qui a un angle droit, c'est-à-dire un angle mesurant exactement 90 degrés. Le théorème de Pythagore s'applique aux triangles rectangles.
Les médianes d'un triangle sont des segments reliant chaque sommet au milieu du côté opposé. Les bissectrices divisent les angles du triangle en deux angles égaux. Les hauteurs sont des segments perpendiculaires aux côtés opposés à partir de chaque sommet.
Les fonctions trigonométriques (sinus, cosinus, tangente, etc.) sont souvent utilisées pour résoudre des problèmes impliquant des triangles. Lois des Triangles : La Loi des cosinus et la Loi des sinus sont utilisées pour résoudre des triangles quelconques. Les triangles sont omniprésents en mathématiques et ont des applications dans de nombreux domaines tels que la trigonométrie, la géométrie analytique, la géométrie projective, et bien d'autres. Les propriétés et les théorèmes liés aux triangles jouent un rôle central dans l'étude de la géométrie. En géométrie, un triangle est une figure plane composée de trois côtés et trois angles. C'est le polygone le plus simple et le plus fondamental. Voici quelques caractéristiques importantes des triangles en géométrie :
Un triangle a trois côtés et trois sommets. Chaque côté est formé par deux sommets adjacents, et chaque sommet est le point de rencontre de deux côtés adjacents.
Triangle Équilatéral : Les trois côtés ont la même longueur. Triangle Isocèle : Au moins deux côtés ont la même longueur. Triangle Scalène : Aucun côté n'a la même longueur que les autres.
La somme des angles intérieurs d'un triangle est toujours 180 degrés (Théorème des angles d'un triangle). Chaque angle extérieur d'un triangle est égal à la somme des deux angles intérieurs non adjacents. Triangles Particuliers : Triangle Rectangle : Un triangle ayant un angle droit (90 degrés). Triangle Obtusangle : Un triangle ayant un angle obtus (supérieur à 90 degrés).Triangle Aigu : Un triangle ayant des angles aigus (inférieurs à 90 degrés).
Applicable aux triangles rectangles, il énonce que dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés. Les triangles sont omniprésents en géométrie, et de nombreux théorèmes et propriétés leur sont associés. Ils sont essentiels pour comprendre et résoudre divers problèmes géométriques. |
Définition graphique
- AUTRES MEDIAS
![]() triangles Les triangles
triangles Les triangles
![]() triangles Les triangles
triangles Les triangles
![]() Représentation graphique spatiale Les triangles
Représentation graphique spatiale Les triangles
 Concepts ou notions associés
Concepts ou notions associés
Géométrie du triangle / Triangulation / Transformation de similitude / Sphère trigonométrique / Théorème de l'inégalité triangulaire / Triangle scalène / Triangle obtusangle / Triangle acutangle / Théorème d'Héron / Triangle de Pascal / Centre de gravité (centroïde) / Théorème de l'angle inscrit / Triangle de Sierpinski / Triangle de Penrose / Triangle aplati /
 Exemples, applications, utilisations
Exemples, applications, utilisations
Dans un triangle rectangle (c'est-à-dire un triangle qui a un angle droit), la base est généralement considérée comme le côté sur lequel repose le triangle. C'est le côté opposé à l'angle droit. Les deux côtés qui forment l'angle droit sont appelés les côtés de la base.
Dans un triangle isocèle (c'est-à-dire un triangle avec au moins deux côtés de même longueur), la base est souvent considérée comme le côté qui n'est pas égal aux deux autres. Les côtés égaux sont appelés les côtés de base. Il est important de noter que dans un triangle quelconque, sans autre spécification, le terme "base" peut ne pas être aussi clairement défini. Le choix de la base dépend souvent du contexte ou de la manière dont le triangle est utilisé dans un problème ou une situation particulière. L'altitude d'un triangle est une droite perpendiculaire à l'un de ses côtés, et elle passe par le sommet opposé à ce côté. En d'autres termes, l'altitude relie un sommet du triangle au côté opposé de manière perpendiculaire.Il existe trois altitudes dans un triangle, chacune associée à l'un des trois côtés. Les points d'intersection des altitudes avec les côtés peuvent être utilisés pour former des segments appelés hauteurs du triangle. Lorsqu'une altitude est tracée depuis un sommet d'un triangle, elle divise ce triangle en deux triangles plus petits, qui peuvent ou non être des triangles rectangles. Les propriétés des triangles obtenus à partir de l'altitude sont souvent utilisées dans la résolution de problèmes géométriques et dans les démonstrations mathématiques.Il est important de noter que l'altitude peut également être appelée hauteur dans certains contextes, en particulier lorsque l'on considère la longueur de la ligne perpendiculaire du sommet au côté opposé. Une médiane d'un triangle est un segment de droite qui relie un sommet du triangle au point moyen (milieu) du côté opposé. Chaque triangle a trois médianes, une émanant de chaque sommet. Les trois médianes d'un triangle se croisent toujours en un point appelé le centre de masse ou le centre de gravité du triangle. Pour trouver le point d'intersection des médianes (le centre de gravité), vous pouvez prendre chaque paire de sommets opposés et tracer le segment de droite qui relie le sommet au milieu du côté opposé. L'intersection de ces trois segments est le centre de gravité.Les médianes ont certaines propriétés intéressantes.Les médianes se croisent toujours au centre de gravité du triangle.Chaque médiane divise le triangle en deux triangles de même aire.Le rapport dans lequel une médiane divise l'autre est 2:1. En d'autres termes, si G est le centre de gravité et M est le milieu du côté opposé, alors GM est deux fois plus long que MG.Les médianes sont largement utilisées dans la géométrie pour déterminer des points importants dans un triangle et pour résoudre divers problèmesgéométriques. La bissectrice d'un angle dans un triangle est une droite ou un segment de droite qui divise cet angle en deux angles égaux ou de même mesure. Chaque angle d'un triangle a une bissectrice, et il y a trois bissectrices dans un triangle, une pour chaque angle.Les propriétés importantes des bissectrices dans un triangle incluent :Intersection en un point : Les trois bissectrices d'un triangle se croisent toujours en un point appelé le centre du cercle inscrit, qui est le centre du cercle inscrit dans le triangle.Divise le côté opposé : Chaque bissectrice divise le côté opposé au sommet dont elle émane en segments proportionnels aux côtés adjacents. En d'autres termes, si une bissectrice émane du sommet A et coupe le côté opposé BC en D, alors BD/CD = AB/AC. Les bissectrices sont souvent utilisées dans des problèmes géométriques et dans la détermination de points importants dans un triangle, comme le centre du cercle inscrit. Ces propriétés sont connues sous le nom de propriétés de la bissectrice intérieure d'un triangle. Il existe également des bissectrices extérieures, mais elles sont moins couramment utilisées. Le théorème de Pythagore est l'un des résultats les plus fondamentaux en géométrie, et il s'applique aux triangles rectangles. Il énonce la relation entre les longueurs des côtés d'un triangle rectangle. Voici la formulation du théorème de Pythagore : Dans un triangle rectangle, le carré de la longueur de l'hypoténuse (le côté opposé à l'angle droit) est égal à la somme des carrés des longueurs des deux autres côtés, appelés les côtés de l'angle droit. Mathématiquement, cela peut être exprimé comme suit : C²=A²+B² où : C est la longueur de l'hypoténuse,A et B sont les longueurs des côtés de l'angle droit. Ce théorème est très utilisé pour résoudre des problèmes impliquant des triangles rectangles et pour vérifier si un triangle est effectivement rectangle. Il a des applications pratiques dans de nombreux domaines, y compris la trigonométrie et la résolution de problèmes liés à la distance et aux mesures dans l'espace. La trigonométrie est une branche des mathématiques qui étudie les relations entre les angles et les côtés des triangles. Elle est largement utilisée pour résoudre des problèmes liés aux triangles, en particulier dans le contexte des triangles rectangles. Voici quelques concepts clés de la trigonométrie liés aux triangles :
Dans un triangle rectangle, les principaux rapports trigonométriques sont définis en utilisant les côtés du triangle. Soient A, B, et C les longueurs des côtés du triangle rectangle, où C est l'hypoténuse, A est le côté adjacent à un angle, et B est le côté opposé à cet angle : sin(θ)= B/C(sinus),cos(θ)= A/C(cosinus),tan(θ)= B/A (tangente).
Les identités trigonométriques sont des équations qui établissent des relations entre les fonctions trigonométriques. Par exemple, la plus célèbre est l'identité de Pythagore : Sin²(θ)+cos²(θ)=1 qui découle du théorème de Pythagore dans un triangle rectangle.Les Fonctions Trigonométriques Inverses : Les fonctions trigonométriques inverses (sin-1 , cos −1, 1tan −1, etc.) sont utilisées pour trouver les angles d'un triangle en fonction des longueurs de ses côtés. Ces lois sont utilisées pour résoudre des triangles quelconques, pas seulement les triangles rectangles.
(ou d'autres formulations similaires). La trigonométrie est un outil puissant pour résoudre une variété de problèmes géométriques, notamment ceux liés aux triangles. Un triangle équilatéral est un type particulier de triangle dans lequel les trois côtés ont la même longueur et tous les angles sont égaux. Plus précisément, dans un triangle équilatéral :
Les propriétés du triangle équilatéral simplifient de nombreux calculs et constructions géométriques. Par exemple, dans un triangle équilatéral, les médianes, les hauteurs et les bissectrices sont toutes superposables et se confondent. De plus, le centre du cercle circonscrit au triangle équilatéral est également le centre de gravité et l'orthocentre. Ces propriétés font du triangle équilatéral un objet géométrique intéressant et souvent utilisé dans divers contextes mathématiques et scientifiques. Un triangle isocèle est un type de triangle dans lequel au moins deux côtés ont la même longueur. Cela signifie que deux des trois côtés du triangle sont égaux entre eux. Ces côtés égaux sont appelés les côtés isocèles, et le troisième côté est appelé le côté non isocèle. En plus de la différence de longueur entre les côtés, un triangle isocèle peut également présenter certaines symétries. Par exemple, les angles opposés aux côtés isocèles sont égaux. Cela signifie que si AB=AC, alors l'angle opposé au côté AB (angle à C) est égal à l'angle opposé au côté AC (angle à B). Les propriétés d'un triangle isocèle peuvent être utilisées pour simplifier les calculs et les constructions géométriques. Par exemple, les médianes d'un triangle isocèle provenant des sommets opposés aux côtés égaux sont également des bissectrices et des hauteurs du triangle. La bissectrice issue du sommet opposé au côté non isocèle divise également l'angle en deux angles égaux. Dans un triangle isocèle : Au moins deux côtés ont la même longueur. Les angles opposés aux côtés isocèles sont égaux. Les médianes, hauteurs et bissectrices spécifiques ont des propriétés particulières dans un triangle isocèle. Triangle rectangle Un triangle rectangle est un type particulier de triangle qui possède un angle droit, c'est-à-dire un angle mesurant exactement 90 degrés. En d'autres termes, un triangle rectangle a un côté qui est perpendiculaire à un autre côté, formant ainsi un angle droit.Les côtés qui forment l'angle droit sont appelés les côtés de l'angle droit, et le côté opposé à l'angle droit est appelé l'hypoténuse. On peut utiliser le théorème de Pythagore dans un triangle rectangle pour décrire la relation entre les longueurs de ses côtés :C²=A²+ B² où :C est la longueur de l'hypoténuse,A et B sont les longueurs des côtés de l'angle droit. Les triangles rectangles sont particulièrement importants en trigonométrie, où les fonctions trigonométriques telles que le sinus, le cosinus et la tangente sont définies en fonction des rapports entre les côtés d'un triangle rectangle. Les côtés adjacents à un angle dans un triangle rectangle sont utilisés pour définir le cosinus, les côtés opposés définissent le sinus, et le rapport entre le côté opposé et le côté adjacent donne la tangente de l'angle. Il n'y a pas un seul "théorème de l'aire dans un triangle" unique, car il existe plusieurs formules pour calculer l'aire d'un triangle en fonction de ses côtés et de ses angles. Voici les formules utilisées pour calculer l'aire d'un triangle :
Aire=1/2×Base×Hauteur
Si A, B, et C sont les longueurs des côtés d'un triangle, et S est le demi-périmètre (c'est-à-dire S= 1/2(a+b+c), alors l'aire (A) peut être calculée avec la formule de Heron :A=racine de[S⋅(S−A)⋅(S−B)⋅(S−C)].
Si A et B sont les longueurs de deux côtés d'un triangle et θ est l'angle entre ces côtés, alors l'aire (A) peut être calculée avec la formule A=1/2×A×B×sin(θ) Il est important de choisir la formule appropriée en fonction des informations dont vous disposez sur le triangle (base et hauteur, côtés, angles, etc.). Les différentes formules offrent une flexibilité pour calculer l'aire en fonction des données disponibles. Le théorème des angles d'un triangle énonce que la somme des trois angles intérieurs d'un triangle est toujours égale à 180 degrés. C'est une propriété fondamentale de la géométrie des triangles et peut être exprimée mathématiquement comme suit : ∠A+∠B+∠C=180° où ∠A, ∠B, et ∠C représentent les mesures des angles intérieurs du triangle, avec ∠A à côté BC,∠B à côté AC, et ∠C à côté AB. Ce théorème est vrai pour tous les triangles, qu'ils soient équilatéraux, isocèles, rectangles ou scalènes. Quelle que soit la forme du triangle, la somme de ses angles intérieurs est constamment égale à 180 degrés. Le théorème des angles d'un triangle est fondamental pour de nombreuses démonstrations et applications en géométrie. Le théorème de l'angle extérieur d'un triangle énonce que l'angle extérieur d'un triangle est égal à la somme des deux angles intérieurs non adjacents à cet angle extérieur. Mathématiquement, cela peut être exprimé comme suit : Mesure de l’angle extérieur = Mesure de l’angle non adjacent 1 + Mesure de l’angle non adjacent 2 ou en utilisant des notations d'angles, si ∠A, ∠B, et ∠C sont les angles intérieurs d'un triangle, alors l'angle extérieur à l'angle ∠A serait égal à ∠B+∠C. Ce théorème est valable pour tous les triangles, qu'ils soient équilatéraux, isocèles, rectangles ou scalènes. Il a des applications importantes en géométrie et est souvent utilisé pour résoudre des problèmes impliquant les angles d'un triangle. Le théorème de la médiane d'un triangle énonce que dans un triangle, chaque médiane divise le côté opposé en deux segments de longueur égale, créant ainsi deux triangles de même aire. En d'autres termes, la médiane d'un triangle équilibre la longueur du côté opposé. Mathématiquement, cela peut être exprimé comme suit : Soit ABC un triangle, et AD une médiane issue du sommet A, où D est le point de la médiane situé sur le côté opposé BC. Alors, la longueur de BD est égale à la longueur de CD, et les aires des triangles ABD et ACD sont égales.Graphiquement, cela peut être illustré comme suit :Aire(△ABD)=Aire(△ACD) Cela est vrai pour chaque médiane dans un triangle, peu importe le sommet à partir duquel elle est tracée. Les médianes jouent un rôle important dans la géométrie des triangles et sont souvent utilisées pour déterminer le centre de masse (ou centre de gravité) d'un triangle, qui est également le point d'intersection des trois médianes. Le théorème de la bissectrice dans un triangle énonce que, dans un triangle, la bissectrice d'un angle divise le côté opposé à cet angle en segments proportionnels aux côtés adjacents à l'angle. Mathématiquement, cela peut être exprimé comme suit : Soit ABC un triangle, et AD la bissectrice de l'angle ∠A, où D est le point où la bissectrice rencontre le côté opposé BC. Alors, le rapport des longueurs des côtés BD et CD est égal au rapport des longueurs des côtés AB et AC, c'est-à-dire :BD/CD= AB/AC Graphiquement, cela signifie que la bissectrice divise le côté opposé en segments dont les longueurs sont proportionnelles aux côtés adjacents à l'angle dont elle est la bissectrice. Ce théorème est utile dans divers contextes géométriques et est souvent utilisé pour résoudre des problèmes liés aux triangles, notamment pour trouver des longueurs ou des rapports de longueurs dans un triangle.
Les architectes utilisent des concepts géométriques, notamment des triangles, pour concevoir des structures stables. La trilatération (utilisant des triangles) est également utilisée pour la localisation précise dans la construction. Les satellites GPS utilisent des principes triangulaires pour déterminer la position précise d'un récepteur GPS. La triangulation est utilisée pour calculer la distance entre le récepteur et plusieurs satellites. Informatique graphique : Les graphiques informatiques utilisent souvent des triangles pour modéliser des surfaces et des objets tridimensionnels. C'est la base de la modélisation 3D. Les géodésiens utilisent la triangulation pour mesurer et cartographier de vastes étendues de terrain. Cela aide à établir des réseaux de points géodésiques pour déterminer des distances et des emplacements précis. En optique, les prismes triangulaires sont utilisés pour décomposer la lumière en ses différentes couleurs (spectre). Dans les sciences naturelles, les biologistes et les géologues utilisent la triangulation pour étudier la distribution des espèces ou analyser des formations géologiques. La navigation utilise des triangles pour déterminer des positions, des capes et des distances. Le triangle de navigation est une application importante en navigation maritime et aérienne. Les charpentiers et les menuisiers utilisent des triangles pour mesurer et couper des angles précis. L'équerre, un instrument basé sur le triangle, est largement utilisée dans ces domaines. Calcul des distances inaccessibles : La méthode de la triangulation est utilisée pour mesurer des distances inaccessibles directement. Par exemple, la mesure de la hauteur d'une montagne à l'aide d'un théodolite. Les ingénieurs électriques utilisent des triangles pour analyser des circuits électriques, en particulier avec les transformateurs et les réseaux électriques. Ces exemples montrent la diversité des applications des triangles dans différents domaines, soulignant leur importance fondamentale en mathématiques appliquées et en sciences appliquées. |
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
Une erreur courante est la croyance que la somme des angles d'un triangle est toujours égale à 180 degrés. C'est vrai dans le cas des triangles euclidiens, mais dans d'autres géométries, cette règle peut ne pas s'appliquer.
Certaines personnes peuvent croire qu'un triangle équilatéral (avec tous les côtés égaux) est toujours aussi équiangulaire (avec tous les angles égaux), ce qui n'est pas nécessairement vrai. De même, un triangle isocèle (avec deux côtés égaux) n'a pas nécessairement des angles égaux.
Une erreur fréquente est de penser que le théorème de Pythagore s'applique à tous les triangles, alors qu'il s'applique spécifiquement aux triangles rectangles.
Conception de triangles dans des espaces non euclidiens
Les croyances sur la géométrie des triangles peuvent varier en fonction de la compréhension de la géométrie euclidienne par rapport à des espaces non euclidiens.
Croire que tous les triangles peuvent être dessinés de manière précise : Certains triangles, comme les triangles sphériques sur une sphère, ne peuvent pas être représentés de manière exacte sur une surface plane sans distorsion.
L'erreur peut souvent résulter de simplifications excessives ou de généralisations incorrectes. Il est essentiel d'avoir une compréhension précise des concepts géométriques pour éviter ces erreurs. Si vous avez une question plus spécifique, n'hésitez pas à la poser !
![]() Confusion possible ou glissement de sens
Confusion possible ou glissement de sens
- Confusion entre la Base - Altitude
- Confusion entre la Bissectrice - Médiane
- Confusion entre lesCôtés - Angles correspondants
- Confusion entre lesCôtés - Angles
- Confusion entre les types de triangles Equilatéral- Isocèle Scalène
- Confusion entre les différentes formules de calcul de l'aire d'un triangle.
- Confusion entre le Théorème de l'angle extérieur - Théorème de l'angle intérieur
- Confusion entre la Somme des angles d'un triangle - Somme des angles d'un quadrilatère
- Confusion entre les Côtés opposés - Côtés adjacents dans les triangles rectangles.
- Confusion entre la Hauteur - Longueur d'un côté dans le calcul de l'aire.
- Confusion entre la Trigonométrie dans un triangle rectangle - Trigonométrie dans un triangle quelconque
- Confusion entre les termes Hypoténus - Côté adjacent dans un triangle rectangle.
- Confusion entre les concepts de Triangle semblable - Triangle congruent (identique)
- Confusion entre les théorèmes de Angle opposé - Angle adjacent dans la trigonométrie.
- Confusion entre les notations de Côtés - Angles dans un triangle (utilisation incorrecte de lettres comme a, b, c pour les côtés et A, B, C pour les *angles).
- Confusion dans l'application de la règle de l'inégalité triangulaire.
- Confusion entre les termes Côté adjacent - Côté opposé dans les fonctions trigonométriques.
- Confusion dans la classification des triangles selon leurs angles Obtus- Droit -Aigu et selon leurs côtés Scalène- Isocèle- Equilatéral
- Confusion entre le périmètre - Aire d'un triangle.
- Confusion dans l'utilisation des fonctions trigonométriques Sinus - Cosinus -Tangente dans des contextes différents.
- Confusion dans l'application du théorème de l'angle inscrit dans le cas de triangles inscrits dans des cercles.
- ....................
 Questions possibles
Questions possibles
- [Généralités sur les Triangles]
Quelles sont les caractéristiques d'un triangle? Qu'est-ce qui distingue un triangle équilatéral d'un triangle isocèle? Comment les triangles sont-ils classifiés en fonction de leurs angles?
- [Propriétés des Triangles]
Quel est le théorème de Pythagore et comment est-il utilisé? Comment les médianes d'un triangle sont-elles liées aux côtés et aux sommets?
- [Applications Pratiques]
Comment les triangles sont-ils utilisés en navigation marine? Expliquez comment la trigonométrie est liée aux triangles.
- [Problèmes Géométriques]
Si vous connaissez les longueurs de deux côtés d'un triangle, comment pouvez-vous trouver la longueur du troisième côté? Comment trouver la mesure d'un angle inconnu dans un triangle en utilisant les propriétés des triangles?
- [Géométrie Analytique]
Comment représentez-vous un triangle dans un système de coordonnées cartésiennes? Comment calculeriez-vous l'aire d'un triangle dont vous connaissez les coordonnées des sommets?
- [Triangles dans la Nature]
Comment les triangles apparaissent-ils dans la structure des cristaux? Pourquoi les abeilles construisent-elles leurs rayons de miel sous forme de triangles?
- [Historique]
Quelle est la signification historique du théorème de Pythagore et comment a-t-il été découvert?
- [Calculs Trigonométriques]
Comment utilisez-vous les fonctions trigonométriques pour résoudre un triangle quelconque? Expliquez comment la loi des cosinus peut être appliquée pour résoudre un triangle. Ces questions abordent divers aspects des triangles, allant des concepts de base aux applications pratiques et aux problèmes plus avancés en géométrie et trigonométrie.
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
L'enseignement des triangles peut être structuré de manière progressive, couvrant à la fois les aspects théoriques et les applications pratiques. Voici une approche suggérée pour l'enseignement des triangles :
- Niveau Élémentaire
- [Reconnaissance des Triangles]
Identifier et nommer les différentes catégories de triangles (équilatéral, isocèle, scalène). Caractéristiques de Base :
- [Comprendre les caractéristiques des triangles (trois côtés, trois angles]
Introduire le vocabulaire : côtés, sommets, angles.
- [Propriétés des Triangles]
Théorème des angles d'un triangle. Explorer les triangles ayant des angles droits.
- Niveau Moyen
- [Triangles Spéciaux]
Explorer les propriétés des triangles rectangles, notamment le théorème de Pythagore. Travailler sur des problèmes impliquant la hauteur, les médianes et les bissectrices.
- [Géométrie Analytique]
Introduire la représentation des triangles dans un système de coordonnées cartésiennes.
- [Applications Pratiques]
Résoudre des problèmes du monde réel impliquant des triangles. Utiliser la trigonométrie pour résoudre des triangles.
- Niveau Avancé
- [Lois des Triangles]
Introduire la loi des cosinus et la loi des sinus pour résoudre des triangles quelconques.
- [Trigonométrie Avancée]
Approfondir les concepts trigonométriques appliqués aux triangles. Travailler sur des problèmes complexes de navigation et de résolution de triangles.
- [Géométrie Projective]
Explorer des concepts avancés liés aux triangles dans des contextes géométriques plus abstraits.
- [Activités Pratiques ]
Projets où les élèves peuvent appliquer leurs connaissances à des projets de conception ou à des problèmes du monde réel. Conseils Supplémentaires : Utiliser des ressources visuelles telles que des modèles, des démonstrations et des logiciels de géométrie dynamique. Encourager la résolution de problèmes pour développer les compétences de raisonnement et de résolution de problèmes. Relier les concepts des triangles à d'autres domaines des mathématiques, de la physique et de la vie quotidienne. L'enseignement des triangles peut être progressif et interactif, encourageant les élèves à explorer et à appliquer les concepts de manière pratique.
Aides et astuces
Enseigner les triangles de manière efficace peut nécessiter des approches didactiques créatives et des astuces pour rendre le sujet intéressant et compréhensible pour les élèves. Voici quelques astuces et conseils pour l'enseignement des triangles :
Utilisez des modèles et des images pour illustrer les différents types de triangles. Encouragez les élèves à dessiner et à manipuler des triangles pour renforcer la compréhension visuelle.
Intégrez des activités pratiques, comme la construction de triangles avec des outils géométriques ou des matériaux tels que des cure-pipes. Utilisez des applications interactives ou des logiciels de géométrie pour permettre aux élèves de manipuler virtuellement des triangles.
Reliez les triangles à des situations de la vie quotidienne ou à des professions spécifiques (architecture, navigation, conception graphique, etc.). Utilisez des exemples du monde réel pour montrer comment les triangles sont utilisés dans divers contextes.
Encouragez les élèves à mener leurs propres enquêtes géométriques liées aux triangles. Posez des questions de recherche telles que "Comment pouvez-vous prouver que la somme des angles d'un triangle est toujours 180 degrés?"
Intégrez des outils technologiques comme les tableaux blancs interactifs, les tablettes, ou des applications de géométrie pour rendre l'apprentissage plus interactif.
Favorisez les discussions en classe sur les concepts des triangles. Encouragez les élèves à expliquer leurs idées aux autres. Utilisez des questions stimulantes comme "Pourquoi les architectes utilisent-ils souvent des triangles dans leurs conceptions?"
Intégrez des problèmes de résolution de problèmes dans lesquels les élèves peuvent appliquer leurs connaissances sur les triangles. Utilisez des énigmes ou des casse-têtes pour stimuler l'intérêt des élèves.
Adaptez votre approche pour répondre aux besoins divers des élèves. Fournissez des activités différenciées pour ceux qui ont besoin de défis supplémentaires ou de soutien supplémentaire.
Intégrez des exemples de triangles provenant de différentes cultures du monde pour montrer la diversité de leur utilisation. Théâtre et Simulation : Organisez des jeux de rôle ou des simulations où les élèves peuvent agir en tant que triangles, médianes, bissectrices, etc., pour comprendre les relations et les propriétés. En combinant la visualisation, les activités pratiques, la technologie éducative et la contextualisation, vous pouvez rendre l'enseignement des triangles plus dynamique et engageant pour les élèves.
Education: Autres liens, sites ou portails
 Bibliographie
Bibliographie
Pour citer cette page: (triangles)
ABROUGUI, M & al, 2023. Les triangles. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/Les_triangles>, consulté le 19, mai, 2025
- ..................
- ..................
- ..................
- ..................
- Sponsors Education
- ....... (Concepts)
- Géométrie du triangle
- Triangulation
- Transformation de similitude
- Sphère trigonométrique
- Théorème de l'inégalité triangulaire
- Triangle scalène
- Triangle obtusangle
- Triangle acutangle
- Théorème d'Héron
- Triangle de Pascal
- Centre de gravité (centroïde)
- Théorème de l'angle inscrit
- Triangle de Sierpinski
- Triangle de Penrose
- Triangle aplati
- Concepts
- Les triangles
- Les triangles (Concepts)
- Fiche conceptuelle didactique