Différences entre versions de « La didactique des mathématique »
| (11 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 37 : | Ligne 37 : | ||
== {{Widget:Definition-ecrite-Fiche}} == | == {{Widget:Definition-ecrite-Fiche}} == | ||
| − | |||
<!-- ******** Début Fiche Didactique Definition ********************--> | <!-- ******** Début Fiche Didactique Definition ********************--> | ||
| Ligne 47 : | Ligne 46 : | ||
{{@}} '''[[Définition de base]]''' | {{@}} '''[[Définition de base]]''' | ||
La didactique des mathématiques est l’étude de la manière dont les mathématiques sont enseignées et apprises. Elle s'intéresse aux méthodes utilisées pour aider les élèves à comprendre les concepts mathématiques et surmonter les difficultés qu'ils rencontrent. | La didactique des mathématiques est l’étude de la manière dont les mathématiques sont enseignées et apprises. Elle s'intéresse aux méthodes utilisées pour aider les élèves à comprendre les concepts mathématiques et surmonter les difficultés qu'ils rencontrent. | ||
| + | Explicitation : Cette définition met l’accent sur l’aspect pratique de la didactique des mathématiques, sans entrer dans les détails théoriques. Elle souligne l’importance de rendre l’apprentissage des mathématiques adapté aux besoins des élèves. | ||
{{@}} '''[[Définition intermédiaire]]''' | {{@}} '''[[Définition intermédiaire]]''' | ||
| − | La | + | La didactique des mathématiques est une branche des sciences de l'éducation qui s'intéresse aux interactions entre les savoirs mathématiques, les élèves et les enseignants. Elle analyse comment les concepts mathématiques, issus de la recherche, sont adaptés pour être enseignés en classe et comment les élèves les apprennent. Cette discipline prend en compte les obstacles cognitifs que les élèves rencontrent et la manière dont les enseignants peuvent ajuster leurs méthodes pour surmonter ces obstacles. |
| + | Explicitation : Cette définition approfondit l’idée de transmission des savoirs en précisant que la didactique des mathématiques étudie aussi la manière dont les élèves peuvent rencontrer des difficultés et comment les enseignants peuvent y répondre par des ajustements pédagogiques | ||
{{@}} '''[[Définition avancée]]''' | {{@}} '''[[Définition avancée]]''' | ||
| − | La | + | La didactique des mathématiques est une discipline des sciences de l’éducation qui analyse les processus d’enseignement et d’apprentissage des mathématiques. Elle se concentre sur la manière dont les savoirs mathématiques sont transformés pour être enseignés et sur les obstacles que les élèves rencontrent dans leur apprentissage. Cette discipline utilise des concepts comme la transposition didactique, qui décrit comment les savoirs mathématiques sont adaptés à l’enseignement scolaire. Elle s’intéresse également à la relation pédagogique entre les enseignants et les élèves, à travers des notions comme le contrat didactique, qui détermine les attentes partagées entre eux. |
| + | Explicitation : La didactique des mathématiques ne se contente pas de décrire la manière dont les mathématiques sont enseignées, mais analyse également comment les savoirs doivent être adaptés pour être compris des élèves, tout en tenant compte des difficultés que ces derniers peuvent rencontrer. | ||
{{@}} '''[[Définition approfondie]]''' | {{@}} '''[[Définition approfondie]]''' | ||
| − | La | + | La didactique des mathématiques est une discipline scientifique interdisciplinaire qui étudie l’enseignement et l’apprentissage des mathématiques à travers l’interaction entre les savoirs mathématiques, les élèves et les enseignants. Elle s’appuie sur des théories comme la transposition didactique, qui décrit comment les savoirs mathématiques sont transformés pour être enseignés. Elle analyse les obstacles épistémologiques (liés à la nature des savoirs mathématiques) et les obstacles didactiques (liés aux méthodes d’enseignement), ainsi que le rôle crucial du contrat didactique dans la relation pédagogique. Cette discipline prend également en compte l’importance des outils pédagogiques, comme les technologies numériques, et des milieux didactiques, où les élèves peuvent interagir avec les savoirs. Enfin, elle met en lumière des concepts comme la zone de développement proximal (Vygotski) et l’apprentissage instrumental (Rabardel), qui expliquent comment l’accompagnement des élèves dans leur apprentissage, en particulier par l’utilisation d’outils, permet de faciliter leur compréhension des concepts mathématiques. |
| − | + | Explicitation : Cette définition approfondie explique que la didactique des mathématiques analyse non seulement comment enseigner les mathématiques, mais aussi comment les savoirs sont transformés et adaptés pour tenir compte des obstacles cognitifs et didactiques des élèves, tout en prenant en considération les outils et environnements d'apprentissage qui facilitent cette adaptation. | |
| − | |||
| − | |||
<!-- ******** Fin Définition Générale ***************************** --> | <!-- ******** Fin Définition Générale ***************************** --> | ||
| Ligne 65 : | Ligne 65 : | ||
|Typologie= <!------------------------------------ Ne pas Modifier --> | |Typologie= <!------------------------------------ Ne pas Modifier --> | ||
<!-- ****************** Commercez les modifications ****************--> | <!-- ****************** Commercez les modifications ****************--> | ||
| − | + | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
}}<!-- ******** Fin Fiche Didactique Définition ******************* --> | }}<!-- ******** Fin Fiche Didactique Définition ******************* --> | ||
| Ligne 92 : | Ligne 86 : | ||
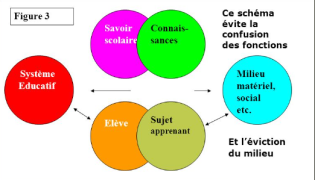
Image:didactique_image11.png|la situation didactique utilise des situations mathématique | Image:didactique_image11.png|la situation didactique utilise des situations mathématique | ||
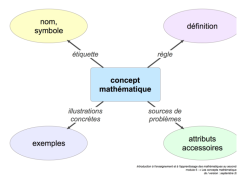
Image:didactique_image12.png|Composantes d’un concept mathématique | Image:didactique_image12.png|Composantes d’un concept mathématique | ||
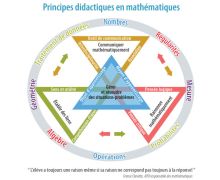
| + | Image:didactique_image13.jpg|principes didactiques en mathémathiques | ||
| + | Image:didactique_image14.jpg|Connaissances mathématiques pour l’enseignement, traduit de Loewenberg Ball et al. (2008) | ||
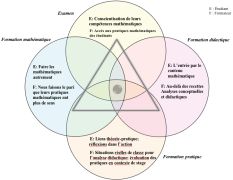
| + | Image:didactique_image15.jpg|Dispositif de formation à l’enseignement des mathématiques : articulation des volets et lieux de formation | ||
</gallery><!-- ************** Fin modification images***************************--> | </gallery><!-- ************** Fin modification images***************************--> | ||
| Ligne 107 : | Ligne 104 : | ||
<youtube width="220" height="220">rIY3c3zeFTw&ab_channel=SVTMAROC</youtube> | <youtube width="220" height="220">rIY3c3zeFTw&ab_channel=SVTMAROC</youtube> | ||
<youtube width="220" height="220">Lc9smnAHL0A&ab_channel=TEDxTalks</youtube> | <youtube width="220" height="220">Lc9smnAHL0A&ab_channel=TEDxTalks</youtube> | ||
| − | <youtube width="220" height="220">Z-HtSDF2jFk&ab_channel=éduscol</youtube> | + | <youtube width="220" height="220">Z-HtSDF2jFk&ab_channel=éduscol</youtube> |
| − | + | <youtube width="220" height="220">fN278BJ6FWE&ab_channel=éduscol</youtube> | |
| + | <youtube width="220" height="220">0_UBkGsdSGc&ab_channel=LeHuffPost</youtube> | ||
<!-- ************************* Début modification AutresMedias******************************************************************--> | <!-- ************************* Début modification AutresMedias******************************************************************--> | ||
| Ligne 126 : | Ligne 124 : | ||
{{Commons}} [https://commons.wikimedia.org/w/index.php?search={{PAGENAMEE}} {{PAGENAME}}] | {{Commons}} [https://commons.wikimedia.org/w/index.php?search={{PAGENAMEE}} {{PAGENAME}}] | ||
{{Goc}} [https://www.goconqr.com/en/search?q={{PAGENAMEE}} {{PAGENAME}}] | {{Goc}} [https://www.goconqr.com/en/search?q={{PAGENAMEE}} {{PAGENAME}}] | ||
| − | {{cc}} Représentation graphique spatiale [https://cmapscloud.ihmc.us:443/rid=20X06TFZG-1NRF6BQ-M9WK76 | + | {{cc}} Représentation graphique spatiale [https://cmapscloud.ihmc.us:443/rid=20X06TFZG-1NRF6BQ-M9WK76 carte conceptuelle (cmap)] |
{{pdf}} Document PDF [https://didaquest.org/w/images/1/12/Didactique_des_math%C3%A9matique.pdf: Document PDF] | {{pdf}} Document PDF [https://didaquest.org/w/images/1/12/Didactique_des_math%C3%A9matique.pdf: Document PDF] | ||
| − | {{fig}} Image/Figure [https:// | + | {{fig}} Image/Figure [https://issuu.com/emilie.c/docs/didactique_des_maths {{PAGENAME}}: didactique des mathématique] |
}}<!-- ************************* Fin modifications pour les Médias *******************************************************--> | }}<!-- ************************* Fin modifications pour les Médias *******************************************************--> | ||
| Ligne 284 : | Ligne 282 : | ||
Un **problème mathématique** est un exercice demandant une résolution spécifique. Une **situation didactique** est un cadre organisé où l’élève interagit avec un savoir en construction (exemple : jouer avec des représentations pour comprendre les fractions). Une **tâche pédagogique** est une activité conçue par l’enseignant dans un objectif d’apprentissage. Ces notions se chevauchent mais ne doivent pas être assimilées de manière interchangeable. | Un **problème mathématique** est un exercice demandant une résolution spécifique. Une **situation didactique** est un cadre organisé où l’élève interagit avec un savoir en construction (exemple : jouer avec des représentations pour comprendre les fractions). Une **tâche pédagogique** est une activité conçue par l’enseignant dans un objectif d’apprentissage. Ces notions se chevauchent mais ne doivent pas être assimilées de manière interchangeable. | ||
| + | {{@}} '''Autres erreurs fréquentes''': | ||
| + | |||
| + | * '''[[Mauvaise interprétation des objectifs pédagogiques]]''': | ||
| + | Il arrive fréquemment que les enseignants mélangent les objectifs de contenu avec les objectifs d'apprentissage. Par exemple, un objectif de contenu pourrait être "comprendre les équations différentielles", tandis qu'un objectif d'apprentissage serait "savoir résoudre une équation différentielle de premier ordre". Confondre ces objectifs peut entraîner une confusion sur la manière dont les élèves doivent aborder l'apprentissage et ce qu'ils sont censés maîtriser à la fin de l'activité. | ||
| + | |||
| + | * '''[[Négligence des prérequis des élèves]]''': | ||
| + | Certains enseignants commettent l'erreur de ne pas vérifier ou prendre en compte les connaissances préalables des élèves avant d'introduire un nouveau concept. Par exemple, enseigner des fractions sans s'assurer que les élèves comprennent les concepts de numérateur et de dénominateur peut conduire à des lacunes profondes. Les prérequis doivent toujours être intégrés à la planification de l'enseignement pour éviter ces lacunes. | ||
| + | |||
| + | * '''[[Utilisation excessive de la pédagogie frontale]]''': | ||
| + | La pédagogie frontale, bien qu'efficace dans certains contextes, peut entraîner une passivité des apprenants si elle est utilisée de manière excessive. Cela peut limiter l'engagement des élèves et leur capacité à appliquer activement les concepts. Il est important de varier les méthodes pédagogiques pour encourager une participation active et une compréhension approfondie des notions. | ||
| − | + | * '''[[Sous-estimation de l'importance de la rétroaction formative]]''': | |
| − | + | La rétroaction formative est essentielle pour guider l'élève tout au long de son apprentissage. Ne pas fournir de rétroaction régulière ou se contenter d’une évaluation sommative (comme des examens) sans retour d’information peut nuire à la progression des apprenants. Les enseignants doivent s'assurer d'offrir des feedbacks constructifs et opportuns pour favoriser une compréhension continue. | |
| − | |||
| + | * '''[[Manque d’adaptation des stratégies d’enseignement]]''': | ||
| + | Les enseignants peuvent parfois adopter une méthode d'enseignement unique, sans tenir compte des divers styles d'apprentissage ou des besoins spécifiques des élèves. Par exemple, certains élèves peuvent être plus visuels, d'autres auditifs ou kinesthésiques. Ne pas diversifier les approches pédagogiques peut rendre l'apprentissage moins accessible pour certains apprenants. | ||
}}<!-- ************** Fin Fiche Didactique Conceptions ********************* --> | }}<!-- ************** Fin Fiche Didactique Conceptions ********************* --> | ||
Version actuelle datée du 18 décembre 2024 à 15:15
 Traduction
Traduction
La didactique des mathématiques (Français) / Mathematics Didactics (Anglais) / تعليم الرياضيات (Arabe) / La didáctica de las matemáticas (Espagnol) / A didática da matemática (Portugais) / Дидактика математики (Russe) / La didattica della matematica (Italien) / Die Didaktik der Mathematik (Allemand) / 数学教学法 (Chinois (Mandarin)) / गणित शिक्षाशास्त्र (Hindi) / 数学の教育学 (Japonais) / গণিত শিক্ষাদান (Bengali).
 Définition
Définition
Domaine, Discipline, Thématique
Définition écrite
![]() Définition de base
La didactique des mathématiques est l’étude de la manière dont les mathématiques sont enseignées et apprises. Elle s'intéresse aux méthodes utilisées pour aider les élèves à comprendre les concepts mathématiques et surmonter les difficultés qu'ils rencontrent.
Explicitation : Cette définition met l’accent sur l’aspect pratique de la didactique des mathématiques, sans entrer dans les détails théoriques. Elle souligne l’importance de rendre l’apprentissage des mathématiques adapté aux besoins des élèves.
Définition de base
La didactique des mathématiques est l’étude de la manière dont les mathématiques sont enseignées et apprises. Elle s'intéresse aux méthodes utilisées pour aider les élèves à comprendre les concepts mathématiques et surmonter les difficultés qu'ils rencontrent.
Explicitation : Cette définition met l’accent sur l’aspect pratique de la didactique des mathématiques, sans entrer dans les détails théoriques. Elle souligne l’importance de rendre l’apprentissage des mathématiques adapté aux besoins des élèves.
![]() Définition intermédiaire
La didactique des mathématiques est une branche des sciences de l'éducation qui s'intéresse aux interactions entre les savoirs mathématiques, les élèves et les enseignants. Elle analyse comment les concepts mathématiques, issus de la recherche, sont adaptés pour être enseignés en classe et comment les élèves les apprennent. Cette discipline prend en compte les obstacles cognitifs que les élèves rencontrent et la manière dont les enseignants peuvent ajuster leurs méthodes pour surmonter ces obstacles.
Explicitation : Cette définition approfondit l’idée de transmission des savoirs en précisant que la didactique des mathématiques étudie aussi la manière dont les élèves peuvent rencontrer des difficultés et comment les enseignants peuvent y répondre par des ajustements pédagogiques
Définition intermédiaire
La didactique des mathématiques est une branche des sciences de l'éducation qui s'intéresse aux interactions entre les savoirs mathématiques, les élèves et les enseignants. Elle analyse comment les concepts mathématiques, issus de la recherche, sont adaptés pour être enseignés en classe et comment les élèves les apprennent. Cette discipline prend en compte les obstacles cognitifs que les élèves rencontrent et la manière dont les enseignants peuvent ajuster leurs méthodes pour surmonter ces obstacles.
Explicitation : Cette définition approfondit l’idée de transmission des savoirs en précisant que la didactique des mathématiques étudie aussi la manière dont les élèves peuvent rencontrer des difficultés et comment les enseignants peuvent y répondre par des ajustements pédagogiques
![]() Définition avancée
La didactique des mathématiques est une discipline des sciences de l’éducation qui analyse les processus d’enseignement et d’apprentissage des mathématiques. Elle se concentre sur la manière dont les savoirs mathématiques sont transformés pour être enseignés et sur les obstacles que les élèves rencontrent dans leur apprentissage. Cette discipline utilise des concepts comme la transposition didactique, qui décrit comment les savoirs mathématiques sont adaptés à l’enseignement scolaire. Elle s’intéresse également à la relation pédagogique entre les enseignants et les élèves, à travers des notions comme le contrat didactique, qui détermine les attentes partagées entre eux.
Explicitation : La didactique des mathématiques ne se contente pas de décrire la manière dont les mathématiques sont enseignées, mais analyse également comment les savoirs doivent être adaptés pour être compris des élèves, tout en tenant compte des difficultés que ces derniers peuvent rencontrer.
Définition avancée
La didactique des mathématiques est une discipline des sciences de l’éducation qui analyse les processus d’enseignement et d’apprentissage des mathématiques. Elle se concentre sur la manière dont les savoirs mathématiques sont transformés pour être enseignés et sur les obstacles que les élèves rencontrent dans leur apprentissage. Cette discipline utilise des concepts comme la transposition didactique, qui décrit comment les savoirs mathématiques sont adaptés à l’enseignement scolaire. Elle s’intéresse également à la relation pédagogique entre les enseignants et les élèves, à travers des notions comme le contrat didactique, qui détermine les attentes partagées entre eux.
Explicitation : La didactique des mathématiques ne se contente pas de décrire la manière dont les mathématiques sont enseignées, mais analyse également comment les savoirs doivent être adaptés pour être compris des élèves, tout en tenant compte des difficultés que ces derniers peuvent rencontrer.
![]() Définition approfondie
La didactique des mathématiques est une discipline scientifique interdisciplinaire qui étudie l’enseignement et l’apprentissage des mathématiques à travers l’interaction entre les savoirs mathématiques, les élèves et les enseignants. Elle s’appuie sur des théories comme la transposition didactique, qui décrit comment les savoirs mathématiques sont transformés pour être enseignés. Elle analyse les obstacles épistémologiques (liés à la nature des savoirs mathématiques) et les obstacles didactiques (liés aux méthodes d’enseignement), ainsi que le rôle crucial du contrat didactique dans la relation pédagogique. Cette discipline prend également en compte l’importance des outils pédagogiques, comme les technologies numériques, et des milieux didactiques, où les élèves peuvent interagir avec les savoirs. Enfin, elle met en lumière des concepts comme la zone de développement proximal (Vygotski) et l’apprentissage instrumental (Rabardel), qui expliquent comment l’accompagnement des élèves dans leur apprentissage, en particulier par l’utilisation d’outils, permet de faciliter leur compréhension des concepts mathématiques.
Explicitation : Cette définition approfondie explique que la didactique des mathématiques analyse non seulement comment enseigner les mathématiques, mais aussi comment les savoirs sont transformés et adaptés pour tenir compte des obstacles cognitifs et didactiques des élèves, tout en prenant en considération les outils et environnements d'apprentissage qui facilitent cette adaptation.
Définition approfondie
La didactique des mathématiques est une discipline scientifique interdisciplinaire qui étudie l’enseignement et l’apprentissage des mathématiques à travers l’interaction entre les savoirs mathématiques, les élèves et les enseignants. Elle s’appuie sur des théories comme la transposition didactique, qui décrit comment les savoirs mathématiques sont transformés pour être enseignés. Elle analyse les obstacles épistémologiques (liés à la nature des savoirs mathématiques) et les obstacles didactiques (liés aux méthodes d’enseignement), ainsi que le rôle crucial du contrat didactique dans la relation pédagogique. Cette discipline prend également en compte l’importance des outils pédagogiques, comme les technologies numériques, et des milieux didactiques, où les élèves peuvent interagir avec les savoirs. Enfin, elle met en lumière des concepts comme la zone de développement proximal (Vygotski) et l’apprentissage instrumental (Rabardel), qui expliquent comment l’accompagnement des élèves dans leur apprentissage, en particulier par l’utilisation d’outils, permet de faciliter leur compréhension des concepts mathématiques.
Explicitation : Cette définition approfondie explique que la didactique des mathématiques analyse non seulement comment enseigner les mathématiques, mais aussi comment les savoirs sont transformés et adaptés pour tenir compte des obstacles cognitifs et didactiques des élèves, tout en prenant en considération les outils et environnements d'apprentissage qui facilitent cette adaptation.
Définition graphique
- AUTRES MEDIAS
![]() La didactique des mathématique (Discipline)
La didactique des mathématique (Discipline)
![]() La didactique des mathématique: (Discipline)
La didactique des mathématique: (Discipline)
![]() La didactique des mathématique: (Discipline)
La didactique des mathématique: (Discipline)
![]() La didactique des mathématique: (Discipline)
La didactique des mathématique: (Discipline)
![]() La didactique des mathématique: (Discipline)
La didactique des mathématique: (Discipline)
![]() La didactique des mathématique
La didactique des mathématique
![]() La didactique des mathématique
La didactique des mathématique
![]() Représentation graphique spatiale carte conceptuelle (cmap)
Représentation graphique spatiale carte conceptuelle (cmap)
![]() Document PDF Document PDF
Document PDF Document PDF
![]() Image/Figure La didactique des mathématique: didactique des mathématique
Image/Figure La didactique des mathématique: didactique des mathématique
 Concepts ou notions associés
Concepts ou notions associés
Apprentissage / Enseignement / Pédagogie / Cognition / Motivation / Évaluation / Connaissance / Compétence / Obstacle / Erreur / Méthodologie / Conceptualisation / Représentation / Raisonnement / Stratégie / Progression / Modélisation / Séquence / Situation-problème / Théorie / Interaction / Didactique / Contexte / Compétence / Outil /
 Exemples, applications, utilisations
Exemples, applications, utilisations
|
 Erreurs ou confusions éventuelles
Erreurs ou confusions éventuelles
![]() Exemples de difficultés de compréhension ou d'interprétation courantes:
Exemples de difficultés de compréhension ou d'interprétation courantes:
Beaucoup d'étudiants confondent la didactique avec la pédagogie. La didactique se concentre sur les contenus d'enseignement et leur organisation, tandis que la pédagogie s'intéresse davantage aux méthodes et aux pratiques d'enseignement en fonction des apprenants.
Les concepts mathématiques sont souvent abstraits, ce qui rend leur étude didactique particulièrement ardue. Par exemple, enseigner les fractions ou l'infini peut poser des défis différents selon les niveaux cognitifs et les préconceptions des apprenants.
Les erreurs des apprenants ne sont pas toujours des échecs, mais peuvent être des indicateurs d'obstacles épistémologiques ou didactiques. Il est essentiel de distinguer ces notions pour adapter les stratégies d'enseignement.
Les enseignants peuvent avoir du mal à appliquer les théories complexes comme la théorie des situations didactiques de Brousseau ou la notion de contrat didactique, en particulier si elles ne sont pas bien expliquées ou contextualisées.
Les apprenants peuvent mal comprendre les interactions entre schémas de connaissances existants et nouveaux. Cela peut conduire à des amalgames, par exemple entre la notion de proportionnalité et celle de linéarité.
Il est souvent difficile pour les enseignants de prendre conscience de leurs propres biais ou pratiques implicites, qui peuvent influencer la manière dont les contenus mathématiques sont transmis et reçus.
Le triangle didactique (enseignant, apprenant, savoir) peut être difficile à modéliser dans la pratique, notamment dans les situations où l'un des sommets (par exemple, l'apprenant) ne joue pas le rôle attendu.
La spécificité du langage mathématique (notations, symboles, terminologie) peut être une barrière pour les apprenants, rendant difficile leur appropriation des concepts, et cela complique leur analyse en didactique.
Certains enseignants peuvent être réticents à modifier leurs pratiques d'enseignement des mathématiques en fonction des recherches en didactique, par peur de perdre du contrôle ou de devoir réapprendre leurs propres méthodes.
![]() Confusions ou glissement de sens potentiels
Confusions ou glissement de sens potentiels
Une confusion fréquente réside dans l’interprétation des termes "didactique" et "pédagogie". La didactique traite spécifiquement de l'étude et de l'organisation des contenus mathématiques dans le but de faciliter leur enseignement et apprentissage, tandis que la pédagogie englobe les méthodes générales de transmission des savoirs et les relations éducatives. Par exemple, penser que "choisir une activité ludique" relève de la didactique est un glissement erroné, car cela relève davantage de choix pédagogiques.
Ces trois notions sont souvent confondues. Une **erreur** est un résultat inattendu mais explicable, souvent lié à un raisonnement incorrect. Un **obstacle**, en revanche, est une difficulté structurelle ou conceptuelle qui empêche la progression de l’apprentissage (exemple : le concept d'infini). Un **concept mal défini** résulte de la mauvaise présentation ou du flou dans l’explication initiale. Ces distinctions sont importantes pour diagnostiquer et remédier correctement aux problèmes d'apprentissage.
Ces trois dimensions du savoir sont parfois amalgamées. Le savoir savant est la version formelle et théorique produite par les experts (mathématiciens), le savoir enseigné correspond à l’adaptation faite par l’enseignant pour le transmettre, et le savoir appris est ce que l’élève finit par comprendre et intégrer. Par exemple, on peut enseigner une simplification d’un théorème, mais l'élève peut en comprendre encore une version réduite, voire erronée.
Le **contrat didactique** désigne les attentes implicites et explicites entre enseignant et apprenant dans une situation d’enseignement. La **transposition didactique**, quant à elle, désigne le processus de transformation du savoir savant en savoir enseigné. Confondre ces notions revient à mal interpréter la dynamique entre ce qui est enseigné et comment il est appris.
Un **problème mathématique** est un exercice demandant une résolution spécifique. Une **situation didactique** est un cadre organisé où l’élève interagit avec un savoir en construction (exemple : jouer avec des représentations pour comprendre les fractions). Une **tâche pédagogique** est une activité conçue par l’enseignant dans un objectif d’apprentissage. Ces notions se chevauchent mais ne doivent pas être assimilées de manière interchangeable.
Il arrive fréquemment que les enseignants mélangent les objectifs de contenu avec les objectifs d'apprentissage. Par exemple, un objectif de contenu pourrait être "comprendre les équations différentielles", tandis qu'un objectif d'apprentissage serait "savoir résoudre une équation différentielle de premier ordre". Confondre ces objectifs peut entraîner une confusion sur la manière dont les élèves doivent aborder l'apprentissage et ce qu'ils sont censés maîtriser à la fin de l'activité.
Certains enseignants commettent l'erreur de ne pas vérifier ou prendre en compte les connaissances préalables des élèves avant d'introduire un nouveau concept. Par exemple, enseigner des fractions sans s'assurer que les élèves comprennent les concepts de numérateur et de dénominateur peut conduire à des lacunes profondes. Les prérequis doivent toujours être intégrés à la planification de l'enseignement pour éviter ces lacunes.
La pédagogie frontale, bien qu'efficace dans certains contextes, peut entraîner une passivité des apprenants si elle est utilisée de manière excessive. Cela peut limiter l'engagement des élèves et leur capacité à appliquer activement les concepts. Il est important de varier les méthodes pédagogiques pour encourager une participation active et une compréhension approfondie des notions.
La rétroaction formative est essentielle pour guider l'élève tout au long de son apprentissage. Ne pas fournir de rétroaction régulière ou se contenter d’une évaluation sommative (comme des examens) sans retour d’information peut nuire à la progression des apprenants. Les enseignants doivent s'assurer d'offrir des feedbacks constructifs et opportuns pour favoriser une compréhension continue.
Les enseignants peuvent parfois adopter une méthode d'enseignement unique, sans tenir compte des divers styles d'apprentissage ou des besoins spécifiques des élèves. Par exemple, certains élèves peuvent être plus visuels, d'autres auditifs ou kinesthésiques. Ne pas diversifier les approches pédagogiques peut rendre l'apprentissage moins accessible pour certains apprenants.
 Questions possibles
Questions possibles
- Quelle est la différence entre didactique et pédagogie en mathématiques ?: La didactique se concentre sur les méthodes et processus d’apprentissage propres aux mathématiques, tandis que la pédagogie concerne les techniques générales d'enseignement.
- Qu’est-ce qu’un obstacle épistémologique en didactique des mathématiques ?: Un obstacle épistémologique est une difficulté de compréhension liée à la nature même du concept mathématique, comme la transition des nombres entiers aux nombres rationnels.
- Comment distinguer une erreur d’une stratégie d’apprentissage inadaptée ?: Une erreur est souvent ponctuelle et spécifique, tandis qu’une stratégie inadaptée se répète et peut montrer que l’élève utilise une méthode incorrecte pour résoudre des problèmes.
- Pourquoi la différenciation pédagogique est-elle difficile à appliquer en mathématiques ?: Elle est complexe car elle nécessite d’adapter l’enseignement à des niveaux de compétence variés, sans compromettre l’harmonie de la progression de l’ensemble de la classe.
- En quoi la théorie des situations didactiques peut-elle poser des difficultés pour les enseignants ?: La théorie demande de créer des situations où les élèves construisent eux-mêmes leurs connaissances, ce qui nécessite de doser précisément les interventions de l’enseignant pour ne pas réduire l’autonomie de l’élève.
- Comment peut-on évaluer la progression des compétences mathématiques des élèves ?: La progression peut être évaluée grâce à des évaluations formatives régulières, qui permettent de suivre l’acquisition des compétences et d’identifier les obstacles rencontrés.
- Pourquoi la distinction entre compétences et connaissances est-elle importante en didactique des mathématiques ?: Les compétences englobent le savoir-faire et l'application, tandis que les connaissances concernent le savoir théorique. Les deux sont nécessaires pour une maîtrise complète des mathématiques.
- Quelles difficultés peuvent surgir avec les contextes de problèmes mathématiques ?: Si le contexte est trop éloigné de l'expérience des élèves ou trop artificiel, il peut rendre le problème moins compréhensible et nuire à la motivation.
- Comment aider les élèves à comprendre des concepts abstraits en mathématiques ?: On peut utiliser des représentations visuelles, des manipulations concrètes, ou des analogies pour rendre les concepts abstraits plus tangibles et compréhensibles.
- Quelles erreurs peuvent survenir lors de la modélisation mathématique ?: Les élèves peuvent mal interpréter la correspondance entre le modèle mathématique et la réalité, ou choisir des variables et des équations inadéquates pour représenter la situation.
 Liaisons enseignements et programmes
Liaisons enseignements et programmes
Idées ou Réflexions liées à son enseignement
- Clarifier la différence entre didactique et pédagogie:
- Stratégie*: Présenter des exemples concrets en distinguant les aspects pédagogiques (ex: gestion de classe, méthodes générales) et didactiques (ex: approche spécifique pour enseigner les fractions).
- Exemple*: En classe, expliquer qu'une méthode pour capter l’attention relève de la pédagogie, alors que la progression des concepts mathématiques fait partie de la didactique des mathématiques.
- Identifier et surmonter les obstacles épistémologiques:
- Stratégie*: Analyser les erreurs fréquentes sur des notions difficiles comme les fractions ou les nombres négatifs. Faire verbaliser aux élèves leur raisonnement pour identifier où leur compréhension diverge de la norme.
- Exemple*: Demander aux élèves d'expliquer pourquoi ils pensent qu’une fraction avec un dénominateur plus grand représente un nombre plus grand, puis clarifier le concept avec des représentations visuelles.
- Différencier erreurs et stratégies inadaptées:
- Stratégie*: Encourager les élèves à expérimenter différentes méthodes de résolution de problèmes et à réfléchir sur leurs choix. Privilégier des discussions collectives pour examiner diverses approches.
- Exemple*: Dans un problème d’équation, proposer une discussion sur les méthodes employées, identifier les erreurs récurrentes et examiner pourquoi certaines stratégies sont inefficaces.
- Utiliser des outils didactiques adaptés:
- Stratégie*: Intégrer des outils numériques de façon progressive et adaptée au niveau des élèves, en expliquant leur rôle et en montrant comment ils peuvent aider à visualiser les concepts mathématiques.
- Exemple*: Utiliser un logiciel de géométrie dynamique pour explorer la symétrie et permettre aux élèves de manipuler les figures pour mieux comprendre.
- Encourager l’évaluation formative:
- Stratégie*: Utiliser des évaluations formatives fréquentes pour identifier les acquis et ajuster l'enseignement en fonction des besoins des élèves.
- Exemple*: À la fin d’une séquence sur les fractions, proposer un quiz rapide et analyser les réponses pour cibler les points à renforcer au prochain cours.
- Aider les élèves à interpréter les concepts abstraits:
- Stratégie*: Proposer des analogies et des représentations concrètes (modèles en trois dimensions, dessins, etc.) pour simplifier les concepts abstraits.
- Exemple*: Pour expliquer les limites en calcul, utiliser l’image d’un objet qui s’approche infiniment d’une ligne sans jamais la toucher.
- Encourager la modélisation avec des exemples concrets:
- Stratégie*: Travailler sur des situations réelles où les élèves peuvent appliquer les mathématiques pour comprendre la modélisation.
- Exemple*: Demander aux élèves de calculer le coût total de différentes quantités de fournitures pour un projet afin de modéliser des équations linéaires.
- Faciliter la distinction entre compétences et connaissances:
- Stratégie*: Mettre en place des activités qui sollicitent autant la maîtrise des procédures (compétences) que la compréhension des concepts (connaissances).
- Exemple*: Lors d’un exercice de résolution d’équations, encourager les élèves à expliquer chaque étape pour s’assurer qu’ils comprennent le "pourquoi" derrière les manipulations.
- Faire appel à des situations-problèmes pour créer du contexte:
- Stratégie*: Utiliser des problèmes tirés de situations de la vie quotidienne pour ancrer les concepts mathématiques dans un contexte compréhensible et motivant.
- Exemple*: En géométrie, demander aux élèves de calculer la quantité de peinture nécessaire pour un mur afin d’illustrer l’application du calcul de surface.
- Utiliser l’apprentissage collaboratif pour surmonter les malentendus:
- Stratégie*: Mettre en place des groupes de travail où les élèves peuvent partager leurs stratégies et se corriger mutuellement.
- Exemple*: Former des équipes pour résoudre des problèmes de géométrie, en les encourageant à discuter et à justifier leurs réponses. Les échanges aident souvent à corriger les erreurs conceptuelles.
Education: Autres liens, sites ou portails
![]() La didactique des mathématique - Formation/Apprentissage: Exemples de plans structurés (+)
La didactique des mathématique - Formation/Apprentissage: Exemples de plans structurés (+)
![]() Ressources éducatives et académiques
Ressources éducatives et académiques
La didactique des mathématique
La didactique des mathématique
La didactique des mathématique
La didactique des mathématique
La_didactique_des_math%C3%A9matique
La_didactique_des_math%C3%A9matique
La_didactique_des_math%C3%A9matique
La_didactique_des_math%C3%A9matique
La_didactique_des_math%C3%A9matique
 Bibliographie
Bibliographie
Pour citer cette page: (didactique des mathématique)
ABROUGUI, M & al, 2024. La didactique des mathématique. In Didaquest [en ligne]. <http:www.didaquest.org/wiki/La_didactique_des_math%C3%A9matique>, consulté le 23, décembre, 2024
- ..................
- ..................
- ..................
- ..................
- Pages utilisant des arguments dupliqués dans les appels de modèle
- Sponsors Education
- Didactique (Concepts)
- Mathématiques (Concepts)
- Psychologie (Concepts)
- Sciences de l'éducation (Concepts)
- Pédagogie (Concepts)
- Sociologie (Concepts)
- Linguistique (Concepts)
- Philosophie (Concepts)
- Anthropologie (Concepts)
- Neurosciences (Concepts)
- Apprentissage
- Enseignement
- Pédagogie
- Cognition
- Motivation
- Évaluation
- Connaissance
- Compétence
- Obstacle
- Erreur
- Méthodologie
- Conceptualisation
- Représentation
- Raisonnement
- Stratégie
- Progression
- Modélisation
- Séquence
- Situation-problème
- Théorie
- Interaction
- Didactique
- Contexte
- Outil
- Concepts
- La didactique des mathématique
- La didactique des mathématique (Concepts)
- Fiche conceptuelle didactique