Triangle

De Didaquest
Aller à la navigationAller à la recherche


Autres Fiches Conceptuelles
Posez une Question


(+)

Target Icon.pngVotre Publicité sur le Réseau Target Icon.png

Puce-didaquest.png Traduction


More-didaquest.png Traductions


Puce-didaquest.png Définition

Domaine, Discipline, Thématique


More-didaquest.png Justification


Définition écrite

Un triangle est une figure géométrique plane délimitée par trois segments de droite, appelés côtés, et formée par trois sommets. La somme des angles intérieurs d'un triangle est toujours égale à 180°.

Si vous souhaitez ajouter des détails supplémentaires, vous pourriez inclure des informations sur les différents types de triangles (équilatéral, isocèle, scalène, etc.), ou encore sur leurs propriétés particulières

Un **triangle** est une figure géométrique plane fondamentale constituée de trois segments de droite appelés **côtés**, qui se rejoignent en trois points distincts appelés **sommets**. Ces trois sommets, nommés en général \( A \), \( B \), et \( C \), sont reliés par les côtés \( AB \), \( BC \), et \( AC \). Le triangle est la forme géométrique la plus simple dans le plan, puisqu'il est défini par le plus petit nombre de côtés permettant de former un polygone.

  • Propriétés générales du triangle :
1. **Somme des angles** : La somme des trois angles intérieurs d'un triangle est toujours égale à \( 180^\circ \) (ou \(\pi\) radians) dans la géométrie euclidienne.
2. **Types de triangles selon les angles** :
  - **Aigu** : Tous les angles sont strictement inférieurs à \( 90^\circ \).
  - **Droit** : L'un des angles est exactement \( 90^\circ \).
  - **Obtus** : L'un des angles est strictement supérieur à \( 90^\circ \).
3. **Types de triangles selon les côtés** :
  - **Équilatéral** : Les trois côtés ont la même longueur, et les trois angles sont égaux (\(60^\circ\) chacun).
  - **Isocèle** : Deux côtés ont la même longueur, et les angles opposés à ces côtés égaux sont également égaux.
  - **Scalène** : Tous les côtés ont des longueurs différentes, et les trois angles sont distincts.

Classification par le nombre de côtés :

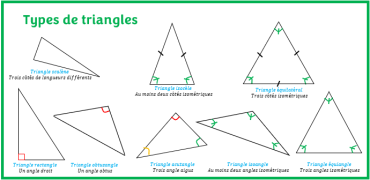
Triangle équilatéral : Trois côtés égaux. Triangle isocèle : Deux côtés égaux. Triangle scalène : Trois côtés de longueurs différentes. Classification par les angles :

Triangle aigu : Trois angles aigus (moins de 90°). Triangle obtus : Un angle obtus (plus de 90°). Triangle rectangle : Un angle droit (exactement 90°). Classification combinée (par côté et par angle) :

Triangle équilatéral acutangle : Un triangle équilatéral avec trois angles aigus. Triangle isocèle rectangle : Un triangle ayant deux côtés égaux et un angle droit }}

Définition graphique

{{Fiche Didactique Media <les triangles > |Galerie Images=

  • Types de triangles

  • Caractéristique d un triangle.png

    les caractéristique d un triangle

  • Titre de Votre Image 3

|Video=

|AutresMedias= |AutresMedias=

  • AUTRES MEDIAS


Google-logo.png Triangle (Discipline)
Bing.png Triangle: (Discipline)
Youtube-didaquest.png Triangle: (Discipline)
Vimeo-logo-didaquest.png Triangle: (Discipline)
Mindmeister-logo-didaquest.png Triangle: (Discipline)
Commons-logo-35px.png Triangle
Goconqr-logo.png Triangle
Ing-connaissance.png Représentation graphique spatiale Triangle: carte conceptuelle (cmap)
Pdf-didaquest.png Document PDF Triangle: Document PDF
Img.png Image/Figure Triangle: Titre de l'image ou de la figure }}

Puce-didaquest.png Concepts ou notions associés

Il semble que tu travailles sur une fiche didactique concernant les triangles. Si tu veux ajouter des mots-clés, voici un exemple que tu pourrais utiliser pour structurer ta fiche :

|Mot-Clé-1=Triangle équilatéral| |Mot-Clé-2=Propriétés des triangles| |Mot-Clé-3=Angle intérieur| |Mot-Clé-4=Pythagore| |Mot-Clé-5=Triangles isocèles| |Mot-Clé-6=Triangles scalènes| |Mot-Clé-7=Somme des angles| |Mot-Clé-8=Classification des triangles| |Mot-Clé-9=Aire d'un triangle| |Mot-Clé-10=Théorème de Pythagore|

Cela devrait couvrir plusieurs concepts importants relatifs aux triangles. Si tu veux personnaliser davantage les mots-clés ou en ajouter d’autres spécifiques à ton programme, n’hésite pas à me le dire ! FIN Fiche Didactique Mots-clés *******************-->

Puce-didaquest.png Exemples, applications, utilisations

Un triangle équilatéral a trois côtés égaux et trois angles de 60°. Par exemple, si l'on considère un triangle avec des côtés de 5 cm, on peut utiliser la formule de l'aire d’un triangle pour calculer son aire : 𝐴 = 3 4 × 𝑎 2 A= 4 3 ​

​ 

×a

2 

, où a est la longueur du côté.

Lorsqu'on étudie les triangles isocèles, on peut utiliser les propriétés des angles à la base pour démontrer des théorèmes géométriques. Par exemple, dans un triangle isocèle avec une base de 8 cm et une hauteur de 6 cm, on peut calculer l’aire en utilisant la formule classique : 𝐴 = 1 2 × 𝑏 𝑎 𝑠 𝑒 × ℎ 𝑎 𝑢 𝑡 𝑒 𝑢 𝑟 A= 2 1 ​ 

×base×hauteur.

Le théorème de Pythagore peut être appliqué pour déterminer la longueur d’un côté dans un triangle rectangle. Si un triangle a des côtés de 3 cm et 4 cm, on peut utiliser 𝑎 2 + 𝑏 2 = 𝑐 2 a 2 

+b

2 

=c

2 

 pour trouver la longueur de l’hypoténuse, ici 5 cm.

La somme des angles intérieurs d'un triangle est toujours égale à 180°. En pratiquant avec des triangles scalènes, on peut vérifier cette propriété en mesurant les angles et en les additionnant. Lorsqu'on travaille avec des triangles dans des contextes de construction ou de design, par exemple, on utilise souvent les propriétés de symétrie et les théorèmes de géométrie pour garantir que les structures sont équilibrées et solides Fin Fiche Didactique Explicitations ******************* -->

Puce-didaquest.png Erreurs ou confusions éventuelles

Emblem-important-blue.svg


Blue-circle-target.png Exemples de difficultés de compréhension ou d'interprétation courantes: Voici une liste des confusions, nuances, erreurs scientifiques et difficultés possibles dans l'enseignement du concept "TRIANGLE" :

  • Confusion entre triangle et autres polygones: Certains élèves ont du mal à distinguer un triangle d’autres polygones comme les quadrilatères ou les trapèzes, en particulier si les figures sont mal dessinées ou déformées.
  • Mauvaise identification des côtés et angles: Les élèves peuvent inverser les notions de côtés et d’angles. Par exemple, confondre la base avec un côté non horizontal ou ne pas comprendre que la hauteur est perpendiculaire à la base.
  • Erreur dans l'application des formules: Les élèves peuvent appliquer de manière incorrecte la formule de la surface, par exemple en oubliant le facteur \(\frac{1}{2}\) ou en confondant la base avec un côté arbitraire.
  • Non-respect des conditions de construction: Certains élèves ne comprennent pas que la somme des longueurs de deux côtés doit toujours être supérieure à la longueur du troisième côté pour former un triangle.
  • Interprétation erronée de la somme des angles: Certains élèves peuvent mal comprendre que la somme des angles d’un triangle est toujours \(180^\circ\), particulièrement lorsqu’ils travaillent dans des géométries non euclidiennes.
  • Erreur de triangulation: Dans des contextes comme la géométrie analytique, les élèves peuvent confondre les coordonnées des sommets et mal appliquer les formules pour trouver la surface.
  • Incompréhension des triangles déformés: Lorsqu’un triangle est dessiné de manière disproportionnée ou mal orientée, cela peut perturber les élèves, qui peuvent ne pas reconnaître immédiatement ses caractéristiques.
  • Difficultés liées à la trigonométrie: Lorsqu’il faut utiliser des fonctions trigonométriques pour calculer la surface d’un triangle, certains élèves peuvent être déstabilisés par les calculs impliquant sinus ou cosinus.
  • Manque de contextualisation pratique: Les élèves peuvent avoir du mal à comprendre l’utilité du concept de triangle lorsqu’il n’est pas relié à des applications concrètes comme l’architecture ou la topographie.

Ces difficultés, bien que variées, peuvent être surmontées par une pédagogie adaptée, combinant des explications claires, des exemples concrets et des exercices pratiques.


Ces confusions, bien que fréquentes, peuvent être levées grâce à des comparaisons explicites et à des exemples clairs lors de l’enseignement.


Blue-circle-target.png Confusions ou glissement de sens potentiels Voici des confusions ou glissements de sens fréquents relatifs au concept "TRIANGLE" :

  • Triangle rectangle - Triangle quelconque : Les élèves peuvent penser que le théorème de Pythagore s’applique à tous les triangles, confondant les triangles rectangles avec des triangles quelconques.
  • Base d'un triangle - Hauteur d'un triangle : Certains élèves croient que la base et la hauteur sont toujours les deux côtés adjacents d’un triangle rectangle, sans comprendre que la hauteur peut être extérieure ou tomber perpendiculairement sur un côté arbitraire.
  • Triangle équilatéral - Triangle isocèle : Les élèves confondent ces deux types de triangles, croyant que tout triangle isocèle est équilatéral, alors qu’un triangle équilatéral est un cas particulier d’un triangle isocèle.
  • Angle aigu - Angle obtus : Il peut y avoir confusion dans la distinction entre un angle aigu et un angle obtus, ce qui conduit à mal classer les triangles aigus ou obtus.
  • Somme des angles - Types de triangles : Les élèves peuvent croire à tort que la somme des angles intérieurs d’un triangle est différente selon son type (équilatéral, isocèle, rectangle), alors qu’elle est toujours \(180^\circ\) en géométrie euclidienne.
  • Hauteur - Médiane - Bissectrice : Ces notions sont souvent confondues, car elles peuvent toutes être des segments reliant un sommet au côté opposé. Cependant, elles ont des définitions et des rôles distincts.
  • Périmètre - Aire : Les élèves mélangent parfois ces concepts, croyant que le périmètre et l’aire d’un triangle sont calculés avec des formules similaires ou qu’ils mesurent des propriétés équivalentes.
  • Triangle - Polygone : Certains élèves généralisent les propriétés des triangles (comme la somme des angles) à tous les polygones, ou inversément, attribuent des propriétés de polygones complexes aux triangles.
  • Triangle plat - Triangle valide : Lorsqu’un triangle a une hauteur proche de zéro (aplatissement), les élèves peuvent croire à tort qu’il ne s’agit plus d’un triangle.
  • Triangle inscrit - Triangle circonscrit : Ces notions géométriques peuvent être confondues, car elles impliquent toutes deux des relations entre un triangle et un cercle, mais elles concernent des configurations opposées.
  • Trigonométrie - Géométrie élémentaire : Certains élèves pensent que la trigonométrie est nécessaire pour calculer l’aire de tout triangle, sans comprendre que la formule classique \(\frac{1}{2} \times \text{base} \times \text{hauteur}\) suffit souvent.


Blue-circle-target.png Autres erreurs fréquentes:

  • .........................................
  • .........................................

(+)



Puce-didaquest.png Questions possibles

Quel est la différence entre un triangle équilatéral et un triangle isocèle ? Comment peut-on déterminer l'aire d'un triangle à partir de ses côtés ? Quelles sont les conditions nécessaires pour qu'un triangle soit rectangle ? Pourquoi la somme des angles intérieurs d’un triangle est-elle toujours égale à 180° ? Comment utiliser le théorème de Pythagore pour vérifier si un triangle est rectangle ? }}

Puce-didaquest.png Liaisons enseignements et programmes

Idées ou Réflexions liées à son enseignement

*  Utiliser des supports visuels (comme des modèles en 3D) pour mieux expliquer les propriétés des triangles. :* Cela aide les élèves à visualiser la géométrie et à comprendre la relation entre les côtés et les angles.
  • Introduire des jeux interactifs pour pratiquer la classification des triangles. :* Par exemple, une activité où les élèves doivent identifier les différents types de triangles à partir de leurs mesures et les classer selon les critères donnés.
  • Encourager les élèves à créer des figures géométriques eux-mêmes, en traçant des triangles à l'aide de compas et de règles. :* Cela leur permet d'expérimenter de manière pratique avec les propriétés des triangles.
  • Intégrer des applications concrètes des triangles dans la vie quotidienne (architecture, design, etc.). :* Par exemple, en discutant de l’utilisation des triangles dans la construction de ponts ou dans des œuvres d'art célèbres.
  • Organiser des mini-projets où les élèves calculent l'aire et le périmètre de triangles dans différents contextes (comme la conception d'un jardin ou la réalisation d'un modèle réduit)

}}

Education: Autres liens, sites ou portails




Puce-didaquest.png Bibliographie

      Géométrie pour les élèves du secondaire de Jean-Marie Moiroux
  • Ce livre aborde les concepts fondamentaux de la géométrie, avec des exercices pratiques sur les triangles et leur classification.

La géométrie pour tous de Pierre-Jean Richet

  • Une ressource accessible aux étudiants de tous niveaux, qui propose des explications détaillées sur les propriétés des triangles, accompagnées d'exemples.

Mathématiques : Cours et exercices corrigés de Gérard Boudon

  • Un ouvrage complet avec des exercices sur les triangles et des applications concrètes.

Les figures géométriques et leurs propriétés de Françoise Chatel

  • Ce livre présente une approche didactique des différentes figures géométriques, avec une attention particulière aux triangles.

L'enseignement de la géométrie à l'école de Michel Serres

  • Un ouvrage utile pour les enseignants, avec des stratégies pédagogiques pour enseigner la géométrie et les triangles aux élèves

}}

Récupérée de « https://didaquest.org/w/index.php?title=Triangle&oldid=136643 »